Zadanie nr 4809992
Okrąg o środku 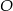 jest styczny do prostej
jest styczny do prostej 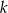 w punkcie
w punkcie 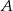 .
.
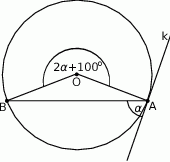
Miara kąta  zaznaczonego na rysunku wynosi
zaznaczonego na rysunku wynosi
A) 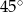 B)
B) 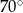 C)
C) 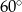 D)
D) 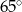
Rozwiązanie
Sposób I
Zauważmy, że
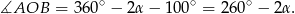
Oczywiście trójkąt 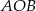 jest trójkątem równoramiennym. Stąd
jest trójkątem równoramiennym. Stąd
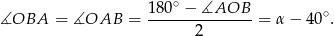
Prosta 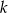 jest styczną okręgu, więc
jest styczną okręgu, więc
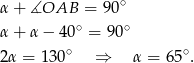
Sposób II
Na mocy twierdzenia o stycznej i siecznej, kąt ostry oparty na cięciwie 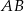 ma miarę
ma miarę  .
.
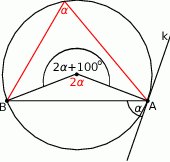
Zatem kąt środkowy oparty na tej samej cięciwie jest dwa razy większy, czyli
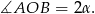
Mamy więc
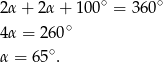
Odpowiedź: D

