Zadanie nr 4957459
Najmniejszą liczbą całkowitą 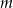 , dla której nierówność:
, dla której nierówność: 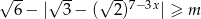 jest sprzeczna jest
jest sprzeczna jest
A) 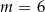 B)
B) 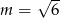 C)
C) 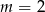 D)
D) 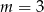
Rozwiązanie
Zbiorem wartości funkcji wykładnicznej postaci 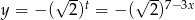 jest przedział
jest przedział 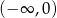 , więc zbiorem wartości wyrażenia
, więc zbiorem wartości wyrażenia 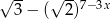 jest przedział
jest przedział 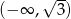 . To z kolei oznacza, że zbiorem wartości
. To z kolei oznacza, że zbiorem wartości 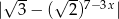 jest przedział
jest przedział 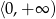 , czyli zbiorem wartości funkcji
, czyli zbiorem wartości funkcji
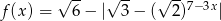
jest przedział 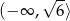 . To oznacza, że nierówność
. To oznacza, że nierówność
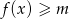
jest sprzeczna gdy 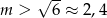 . W takim razie najmniejszą całkowitą wartością
. W takim razie najmniejszą całkowitą wartością 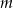 , dla której nierówność jest sprzeczna jest
, dla której nierówność jest sprzeczna jest 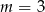 .
.
Na koniec dla ciekawskich wykres lewej strony nierówności.
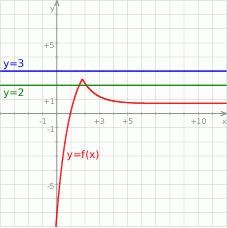
Odpowiedź: D

