Zadanie nr 5089786
Trapez równoramienny 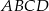 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 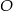 (zobacz rysunek).
(zobacz rysunek).
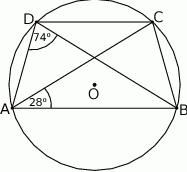
Różnica miar kątów 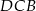 i
i 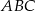 tego trapezu jest równa
tego trapezu jest równa
A) 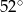 B)
B) 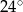 C)
C) 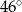 D)
D) 
Rozwiązanie
Sposób I
Korzystamy z tego, że kąty wpisane oparte na tych samych łukach są równe.
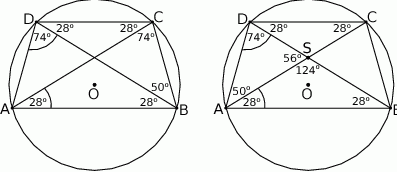
Mamy zatem
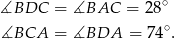
Ponadto 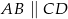 , więc
, więc
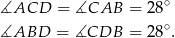
Stąd
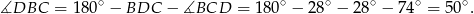
i
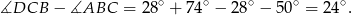
Sposób II
Niech 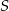 będzie punktem przecięcia się przekątnych trapezu. Trójkąty
będzie punktem przecięcia się przekątnych trapezu. Trójkąty 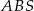 i
i 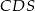 są podobne i równoramienne, więc ich wszystkie kąty ostre mają miary
są podobne i równoramienne, więc ich wszystkie kąty ostre mają miary 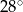 . Ponadto
. Ponadto
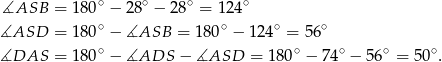
Stąd
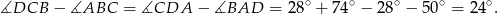
Odpowiedź: B

