Zadanie nr 5131448
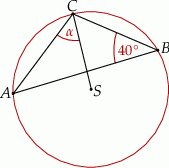
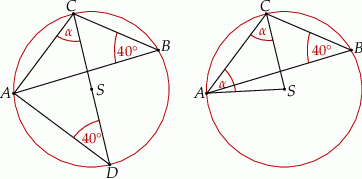
Punkt 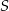 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
A) 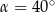 B)
B) 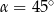 C)
C) 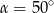 D)
D) 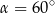
Rozwiązanie
Sposób I
Przedłużmy odcinek 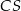 do jego punktu przecięcia
do jego punktu przecięcia 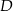 z okręgiem.
z okręgiem.
Kąty 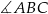 i
i 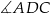 są oparte na tym samym łuku, a kąt
są oparte na tym samym łuku, a kąt 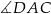 jest oparty na średnicy, więc
jest oparty na średnicy, więc
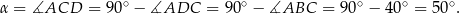
Sposób II
Tym razem dorysujmy promień 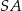 . Kąt
. Kąt 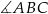 jest kątem wpisanym opartym na tym samym łuku co kąt środkowy
jest kątem wpisanym opartym na tym samym łuku co kąt środkowy 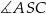 . Zatem
. Zatem
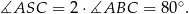
Trójkąt 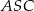 jest równoramienny, więc
jest równoramienny, więc
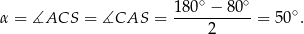
Odpowiedź: C

