/Szkoła średnia/Zadania testowe

Zadanie nr 5134617

Dodaj do ulubionych
Dodaj do rozwiązanych

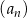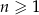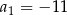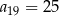W ciągu arytmetycznym (an) , określonym dla n ≥ 1 , dane są dwa wyrazy: a1 = − 1 1 oraz a 19 = 2 5 . Wtedy suma

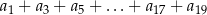
a1 + a 3 + a5 + ...+ a17 + a19

jest równa
A) 133 B) 63 C) 70 D) 49

Rozwiązanie

Sposób I

Interesująca nas suma 10 początkowych wyrazów ciągu 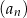(an) o indeksach nieparzystych

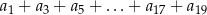
a1 + a 3 + a5 + ...+ a17 + a19

to suma 10 początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie 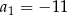a1 = − 11 i różnicy dwa razy większej niż różnica ciągu (an) . Suma ta jest więc równa

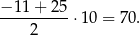
−-11-+-25- 2 ⋅1 0 = 70.

Sposób II

Ze wzoru 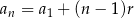an = a1 + (n − 1)r na n -ty wyraz ciągu arytmetycznego mamy

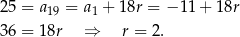
2 5 = a19 = a1 + 18r = − 11 + 18r 3 6 = 18r ⇒ r = 2 .

Interesująca nas suma 10 początkowych wyrazów ciągu 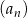(an) o indeksach nieparzystych

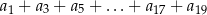
a1 + a 3 + a5 + ...+ a17 + a19

to suma 10 początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie 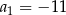a1 = − 11 i różnicy 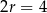2r = 4 . Suma ta jest więc równa

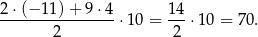
2-⋅(−-11)-+-9-⋅4 ⋅10 = 1-4⋅ 10 = 70. 2 2

 
Odpowiedź: C

Wersja PDF