Zadanie nr 5447695
Dane są wielomiany 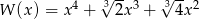 oraz
oraz 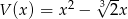 . Wielomian
. Wielomian 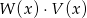 jest równy
jest równy
A) 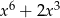 B)
B) 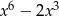 C)
C) 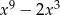 D)
D) 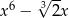
Rozwiązanie
Sposób I
Zauważmy, że na mocy wzoru skróconego mnożenia
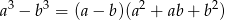
mamy
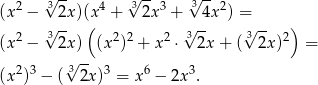
Sposób II
Liczymy
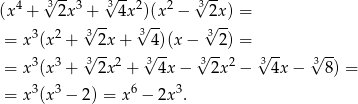
Odpowiedź: B
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dane są wielomiany 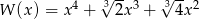 oraz
oraz 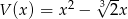 . Wielomian
. Wielomian 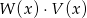 jest równy
jest równy
A) 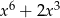 B)
B) 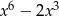 C)
C) 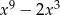 D)
D) 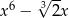
Sposób I
Zauważmy, że na mocy wzoru skróconego mnożenia
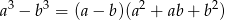
mamy
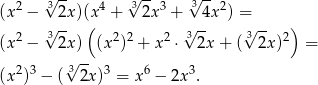
Sposób II
Liczymy
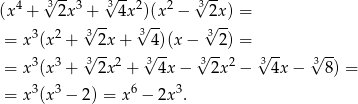
Odpowiedź: B
