Zadanie nr 5488458
Dana jest funkcja kwadratowa 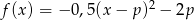 , gdzie
, gdzie 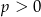 . Wówczas
. Wówczas
A) funkcja osiąga największą wartość równą 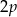 ;
;
B) funkcja ma dwa różne miejsca zerowe;
C) wierzchołek paraboli będącej wykresem 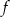 należy do prostej o równaniu
należy do prostej o równaniu 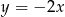 ;
;
D) dla 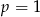 funkcja jest rosnąca w całej swojej dziedzinie.
funkcja jest rosnąca w całej swojej dziedzinie.
Rozwiązanie
Wykresem podanej funkcji jest parabola o ramionach skierowanych w dół (bo współczynnik przy 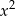 jest ujemny) i wierzchołku w punkcie
jest ujemny) i wierzchołku w punkcie 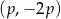 (odczytujemy współrzędne z postaci kanonicznej
(odczytujemy współrzędne z postaci kanonicznej 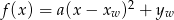 ).
).
- Ponieważ
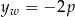 , największą wartością funkcji
, największą wartością funkcji 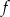 jest
jest 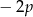 a nie
a nie 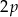 .
. - Dla
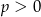 mamy
mamy 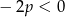 , zatem funkcja jest stale ujemna (oba wyrażenia w wzorze na
, zatem funkcja jest stale ujemna (oba wyrażenia w wzorze na 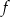 są ujemne).
są ujemne). - Ponieważ
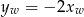 , wierzchołek leży na prostej
, wierzchołek leży na prostej 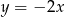 .
. - Dla
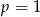 mamy funkcję kwadratową
mamy funkcję kwadratową 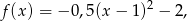
która jest rosnąca na lewo od
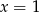 i malejąca na prawo od
i malejąca na prawo od 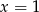 .
.
Odpowiedź: C

