Zadanie nr 5526312
Ze zbioru pięćdziesięciu kolejnych liczb naturalnych od 1 do 50 losujemy dwie liczby  i
i 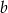 takie, że
takie, że 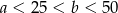 . Prawdopodobieństwo, że liczba
. Prawdopodobieństwo, że liczba 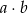 jest podzielna przez 50 jest równe
jest podzielna przez 50 jest równe
A) 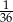 B)
B) 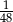 C)
C) 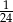 D)
D) 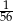
Rozwiązanie
Każdą z liczb  i
i 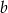 możemy wybrać na 24 sposoby, więc jest
możemy wybrać na 24 sposoby, więc jest
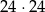
zdarzeń elementarnych (możliwości wyboru takich dwóch liczb). Ponieważ
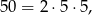
to każda z wylosowanych liczb musi dzielić się przez 5 i przynajmniej jedna z nich musi być parzysta. Jest 12 takich par:
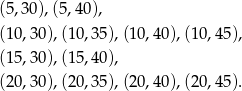
Prawdopodobieństwo jest więc równe
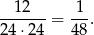
Odpowiedź: B

