/Szkoła średnia/Zadania testowe

Zadanie nr 5551198

Dodaj do ulubionych
Dodaj do rozwiązanych

Funkcja kwadratowa określona jest wzorem 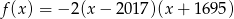f (x) = − 2(x − 20 17)(x+ 1695) . Wynika stąd, że
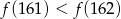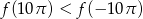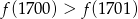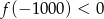
A) f(1 61) < f(16 2) B) f(10π ) < f(− 10 π) C) f(17 00) > f(17 01) D) f (−1 000) < 0

Rozwiązanie

Wykresem danej funkcji jest parabola o ramionach skierowanych w dół i wierzchołku dokładnie w środku między pierwiastkami, czyli w punkcie

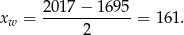
x = 20-17−--1695 = 161. w 2

Funkcja ta jest więc rosnąca na przedziale 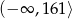(− ∞ ,161 ⟩ i malejąca na przedziale ⟨16 1,+ ∞ ) .

PIC

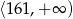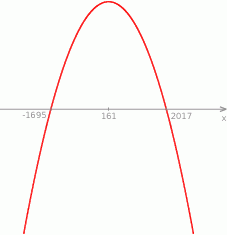
W szczególności

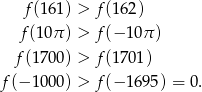
f (161) > f(1 62) f(10π ) > f(− 10 π) f(1 700) > f(1 701) f(− 1 000) > f(− 16 95) = 0.

 
Odpowiedź: C

Wersja PDF