Zadanie nr 5575344
Równanie prostej przechodzącej przez punkty 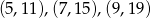 to
to
A) 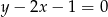 B)
B) 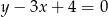 C)
C) 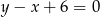 D)
D) 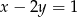
Rozwiązanie
Sposób I
Można zauważyć, że współrzędne podanych punktów spełniają warunek 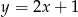 i to jest szukana prosta.
i to jest szukana prosta.
Sposób II
Szukamy prostej postaci 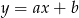 . Aby wyznaczyć
. Aby wyznaczyć  i
i 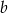 podstawiamy dwa pierwsze punkty.
podstawiamy dwa pierwsze punkty.
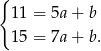
Odejmujemy od drugiego równania pierwsze i mamy 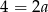 , czyli
, czyli 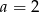 . Z drugiego równania
. Z drugiego równania 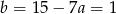 . Zatem szukana prosta to
. Zatem szukana prosta to 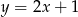 .
.
Sposób III
Korzystamy ze wzoru
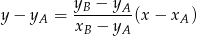
na równanie prostej przechodzącej przez punkty 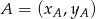 i
i 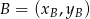 . W naszej sytuacji mamy
. W naszej sytuacji mamy
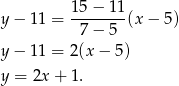
Odpowiedź: A

