/Szkoła średnia/Zadania testowe

Zadanie nr 6342527

Dodaj do ulubionych
Dodaj do rozwiązanych

Jeśli trójkąt prostokątny jest wpisany w okrąg o promieniu 4, a jednym z jego kątów ostrych jest kąt 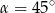α = 45∘ , to pole tego trójkąta jest równe
A) 16 B) 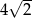√ -- 4 2 C) 8 D)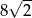 8√ 2-

Rozwiązanie

Zaczynamy od rysunku

PIC

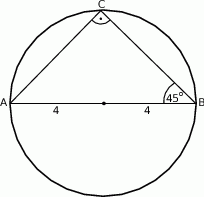
Przeciwprostokątna trójkąta 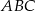ABC jest równa średnicy okręgu (bo kąt prosty w okręgu musi być oparty na średnicy), więc

|AB | = 8.

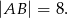
Sposób I

Korzystamy z funkcji cosinus aby wyznaczyć długość boku 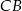CB

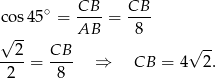
c os45∘ = CB--= CB-- √ -- AB 8 2 CB √ -- ----= ---- ⇒ CB = 4 2. 2 8

Korzystamy z funkcji sinus aby wyznaczyć długość boku 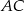AC

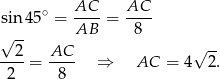
∘ AC-- AC-- sin 45 = AB = 8 √ -- √ -- --2-= AC-- ⇒ AC = 4 2 . 2 8

Liczymy pole powierzchni

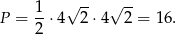
√ -- √ -- P = 1-⋅4 2 ⋅4 2 = 16. 2

Sposób II

Trójkąt o którym mowa w treści to połówka kwadratu o boku 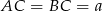AC = BC = a . Wiemy, że przekątna tego kwadratu ma długość 8, więc

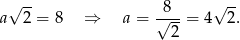
√ -- 8 √ -- a 2 = 8 ⇒ a = √---= 4 2. 2

Zatem pole trójkąta jest równe

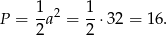
P = 1-a2 = 1-⋅32 = 16. 2 2

 
Odpowiedź: A

Wersja PDF