Zadanie nr 7323954
Z odcinków o długościach: 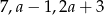 można zbudować trójkąt równoramienny. Wynika stąd, że
można zbudować trójkąt równoramienny. Wynika stąd, że
A) 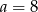 B)
B) 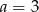 C)
C) 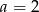 D)
D) 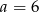
Rozwiązanie
Nie wiemy, które dwa boki trójkąta mają być równe, więc sprawdzamy kolejne możliwości.
Jeżeli 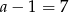 , to
, to 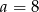 i trzeci bok trójkąta ma długość
i trzeci bok trójkąta ma długość 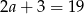 . Tak nie może jednak być, bo nie ma trójkąta o bokach długości: 7, 7, 19.
. Tak nie może jednak być, bo nie ma trójkąta o bokach długości: 7, 7, 19.
Jeżeli 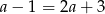 , to
, to 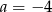 , co nie jest możliwe.
, co nie jest możliwe.
Jeżeli 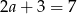 , to
, to 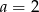 i trzeci bok trójkąta ma długość
i trzeci bok trójkąta ma długość 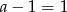 . Otrzymujemy w tej sytuacji trójkąt równoramienny o bokach: 7, 7, 1.
. Otrzymujemy w tej sytuacji trójkąt równoramienny o bokach: 7, 7, 1.
Odpowiedź: C

