/Szkoła średnia/Zadania testowe

Zadanie nr 7448825

Dodaj do ulubionych
Dodaj do rozwiązanych

Równanie 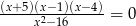(x+5)(x−1)(x−-4) x2−16 = 0
A) nie ma pierwiastków
B) ma jeden pierwiastek
C) ma dwa pierwiastki
D) ma trzy pierwiastki

Rozwiązanie

Korzystamy ze wzoru 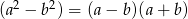2 2 (a − b ) = (a − b)(a + b) i rozpisujemy

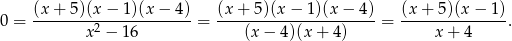
(x+ 5)(x− 1)(x − 4) (x+ 5)(x − 1)(x − 4) (x+ 5)(x − 1) 0 = --------2-------------= ----------------------= --------------. x − 16 (x − 4)(x + 4 ) x + 4

Iloraz jest równy zero jeżeli licznik jest równy zero, czyli

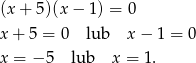
(x + 5)(x− 1) = 0 x+ 5 = 0 lub x − 1 = 0 x = − 5 lub x = 1.

Zatem pierwiastkami równania są 1 i -5 (żadna z tych liczb nie jest miejscem zerowym mianownika).  
Odpowiedź: C

Wersja PDF