/Szkoła średnia/Zadania testowe

Zadanie nr 8371033

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole trójkąta 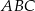ABC o wierzchołkach 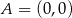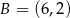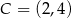A = (0,0) , B = (6,2 ) , C = (2,4) jest równe
A) 10 B) 5 C) 20 D) 15

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

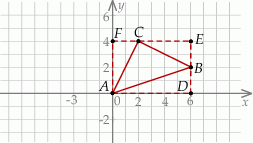
Sposób I

Nawet ze szkicowego rysunku powinno być widać, że trójkąt 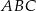ABC ma szanse być prostokątnym. Aby się upewnić, że tak jest, liczymy długości jego boków.

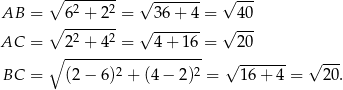
∘ ------- √ ------- √ --- AB = 62 + 22 = 3 6+ 4 = 40 ∘ ------- √ ------- √ --- AC = 22 + 42 = 4 + 1 6 = 20 ∘ ------------------- √ ------- √ --- BC = (2 − 6)2 + (4 − 2)2 = 16 + 4 = 20.

Zatem faktycznie 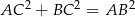AC 2 + BC 2 = AB 2 , czyli trójkąt 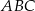ABC jest prostokątny i jego pole wynosi

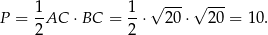
1 1 √ --- √ --- P = --AC ⋅BC = --⋅ 20 ⋅ 20 = 10. 2 2

Sposób II

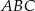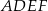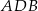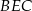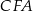Pole trójkąta ABC możemy obliczyć jako różnice pól prostokąta ADEF i trzech trójkątów prostokątnych: ADB , BEC i CFA . Mamy zatem

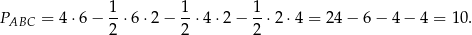
P = 4⋅6 − 1⋅ 6⋅2 − 1-⋅4 ⋅2 − 1-⋅2 ⋅4 = 2 4− 6 − 4 − 4 = 10. ABC 2 2 2

 
Odpowiedź: A

Wersja PDF