/Szkoła średnia/Zadania testowe

Zadanie nr 9806259

Dodaj do ulubionych
Dodaj do rozwiązanych

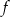Funkcja f jest określona dla wszystkich liczb rzeczywistych wzorem 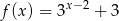f (x) = 3x−2 + 3 . Prosta 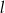l ma równanie 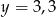y = 3,3 . Ile punktów wspólnych mają wykres funkcji 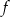f i prosta l ?
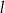A) Zero. B) Jeden. C) Dwa. D) Nieskończenie wiele.

Rozwiązanie

Sposób I

Szkicujemy wykres funkcji 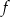f – jest to wykres funkcji wykładniczej 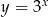x y = 3 przesunięty 2 jednostki w prawo i o trzy do góry.

PIC

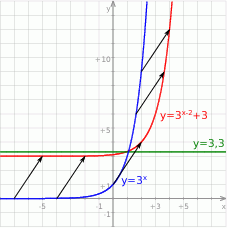
Z rysunku widać, że wykres funkcji 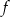f i prosta 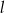l mają jeden punkt wspólny.

Sposób II

Wystarczy ustalić, ile rozwiązań ma równanie

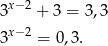
x−2 3 + 3 = 3,3 3x−2 = 0,3.

Ponieważ funkcja wykładnicza jest rosnąca i każda liczba dodatnia jest jej wartością, powyższe równanie ma dokładnie jedno rozwiązanie.  
Odpowiedź: B

Wersja PDF