Suma pierwiastków wielomianu 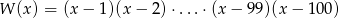 jest równa
jest równa
A) 100 B) 10000 C) 10100 D) 5050
/Szkoła średnia/Zadania testowe/Równania
Suma pierwiastków wielomianu 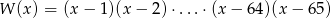 jest równa
jest równa
A) 4290 B) 2145 C) 2080 D) 8580
Suma pierwiastków wielomianu 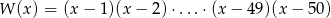 jest równa
jest równa
A) 1275 B) 2550 C) 5100 D) 5050
Dany jest wielomian 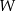 określony wzorem
określony wzorem 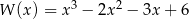 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wielomian
. Wielomian 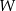 przy rozkładzie na czynniki ma postać
przy rozkładzie na czynniki ma postać
A) 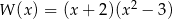 B)
B) 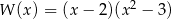
C) 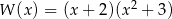 D)
D) 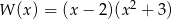
Dany jest wielomian 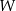 określony wzorem
określony wzorem 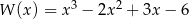 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wielomian
. Wielomian 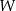 przy rozkładzie na czynniki ma postać
przy rozkładzie na czynniki ma postać
A) 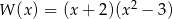 B)
B) 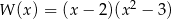
C) 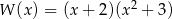 D)
D) 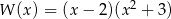
Rozwiązaniem układu równań 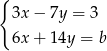 z niewiadomymi
z niewiadomymi  i
i 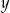 jest para liczb, których suma jest równa 0. Wynika stąd, że
jest para liczb, których suma jest równa 0. Wynika stąd, że
A) 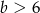 B)
B) 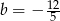 C)
C) 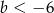 D)
D) 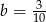
Dla pewnych liczb  i
i 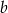 zachodzą równości:
zachodzą równości: 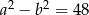 i
i 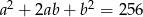 . Dla tych liczb
. Dla tych liczb  i
i 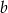 wartość wyrażenia
wartość wyrażenia 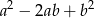 jest równa
jest równa
A) 9 B) 3 C) 18 D) 208
Pierwiastkami równania 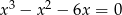 są liczby
są liczby
A) 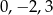 B)
B) 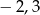 C)
C) 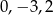 D)
D) 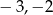
Równanie 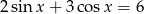 w przedziale
w przedziale 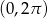
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma więcej niż dwa rozwiązania rzeczywiste.
Równanie 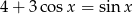 w przedziale
w przedziale 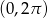
A) ma dokładnie jedno rozwiązanie rzeczywiste.
B) ma dokładnie dwa rozwiązania rzeczywiste.
C) ma więcej niż dwa rozwiązania rzeczywiste.
D) nie ma rozwiązań rzeczywistych.
Równanie 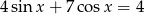
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma więcej niż dwa rozwiązania rzeczywiste.
Dla pewnych liczb  i
i 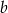 zachodzą równości:
zachodzą równości: 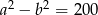 i
i 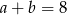 . Dla tych liczb
. Dla tych liczb  i
i 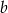 wartość wyrażenia
wartość wyrażenia 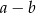 jest równa
jest równa
A) 25 B) 16 C) 10 D) 2
Jeżeli różnica między liczbą  i liczbą
i liczbą 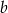 wynosi 5, a różnica między kwadratami tych liczb jest równa 75, to suma tych liczb jest równa
wynosi 5, a różnica między kwadratami tych liczb jest równa 75, to suma tych liczb jest równa
A) 45 B) 35 C) 25 D) 15
Jeżeli 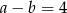 i
i 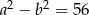 , to
, to 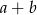 jest równe
jest równe
A) 14 B) 16 C) 18 D) 20
Jeżeli 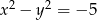 i
i 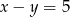 , to wartość wyrażenia
, to wartość wyrażenia 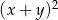 jest równa
jest równa
A) 25 B) 16 C) 9 D) 1
Dla pewnych liczb  i
i 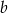 zachodzą równości:
zachodzą równości: 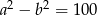 i
i 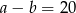 . Dla tych liczb
. Dla tych liczb  i
i 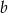 wartość wyrażenia
wartość wyrażenia 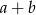 jest równa
jest równa
A) 80 B) 5 C) 10 D) 2
Jeżeli różnica miedzy dwiema liczbami jest równa 5, a różnica między ich kwadratami wynosi 85, to suma tych liczb jest równa
A) 15 B) 16 C) 17 D) 18
Jeżeli 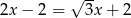 , to
, to
A) 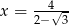 B)
B) 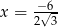 C)
C) 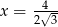 D)
D) 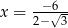
Rozwiązaniem równania 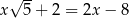 jest liczba
jest liczba
A) 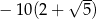 B)
B) 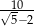 C)
C) 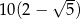 D)
D) 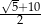
Rozwiązaniem równania 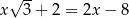 jest liczba
jest liczba
A) 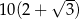 B)
B) 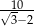 C)
C) 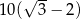 D)
D) 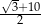
Rozwiązaniem równania 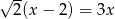 jest liczba
jest liczba
A) 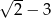 B)
B) 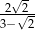 C)
C) 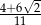 D)
D) 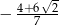
Miejscem zerowym funkcji liniowej 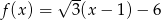 jest liczba
jest liczba
A) 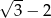 B)
B) 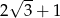 C)
C) 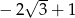 D)
D) 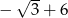
Miejscem zerowym funkcji liniowej 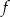 określonej wzorem
określonej wzorem 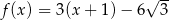 jest liczba
jest liczba
A) 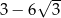 B)
B) 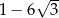 C)
C) 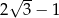 D)
D) 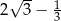
Rozwiązaniem równania 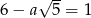 jest liczba
jest liczba
A) 5 B) 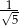 C)
C) 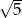 D)
D) 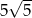
Miejscem zerowym funkcji liniowej 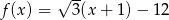 jest liczba
jest liczba
A) 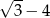 B)
B) 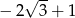 C)
C) 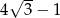 D)
D) 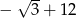
Rozwiązaniem równania 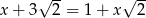 jest liczba
jest liczba
A) 1 B) 2 C) 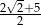 D)
D) 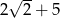
Układ równań 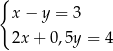 opisuje w układzie współrzędnych na płaszczyźnie
opisuje w układzie współrzędnych na płaszczyźnie
A) zbiór pusty. B) dokładnie jeden punkt.
C) dokładnie dwa różne punkty. D) zbiór nieskończony.
Układ równań 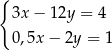 opisuje w układzie współrzędnych na płaszczyźnie
opisuje w układzie współrzędnych na płaszczyźnie
A) zbiór pusty. B) dokładnie jeden punkt.
C) dokładnie dwa różne punkty. D) zbiór nieskończony.
Rozwiązaniem układu równań 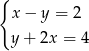 w prostokątnym układzie współrzędnych na płaszczyźnie jest
w prostokątnym układzie współrzędnych na płaszczyźnie jest
A) prosta 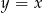 B) dwa punkty C) zbiór pusty D) jeden punkt
B) dwa punkty C) zbiór pusty D) jeden punkt
Na rysunku przedstawiono fragmenty dwóch prostych na płaszczyźnie oraz zaznaczono kilka punktów o współrzędnych całkowitych, przez które przechodzą te proste.
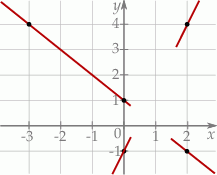
Jeżeli 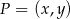 jest punktem wspólnym prostych, których fragmenty przedstawiono na rysunku, to
jest punktem wspólnym prostych, których fragmenty przedstawiono na rysunku, to
A) 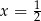 B)
B) 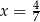 C)
C) 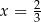 D)
D) 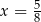
Miejscami zerowymi funkcji kwadratowej 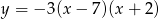 są
są
A) 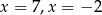 B)
B) 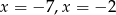 C)
C) 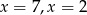 D)
D) 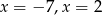
Miejscami zerowymi funkcji kwadratowej 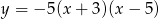 są
są
A) 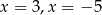 B)
B) 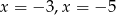 C)
C) 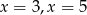 D)
D) 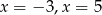
Klient banku wypłacił z bankomatu kwotę 1040 zł. Bankomat wydał kwotę w banknotach o nominałach 20 zł, 50 zł oraz 100 zł. Banknotów 100–złotowych było dwa razy więcej niż 50–złotowych, a banknotów 20–złotowych było o 2 mniej niż 50–złotowych. Niech  oznacza liczbę banknotów 50–złotowych, a
oznacza liczbę banknotów 50–złotowych, a 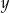 – liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb
– liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb  i
i 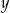 to
to
A) 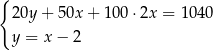 B)
B) 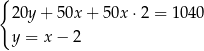
C) 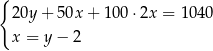 D)
D) 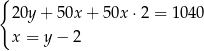
Tomek ma w skarbonce wyłącznie monety dwuzłotowe i pięciozłotowe. W sumie ma w skarbonce 351 zł. Gdyby dołożył do skarbonki 10 monet pięciozłotowych i dwie monety dwuzłotowe, to miałby w skarbonce dwa razy więcej monet dwuzłotowych, niż monet pięciozłotowych. Jeżeli oznaczymy przez  liczbę monet pięciozłotowych, a przez
liczbę monet pięciozłotowych, a przez 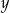 liczbę monet dwuzłotowych w skarbonce Tomka, to liczby
liczbę monet dwuzłotowych w skarbonce Tomka, to liczby  i
i 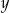 spełniają układ równań
spełniają układ równań
A) 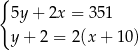 B)
B) 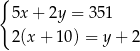
C) 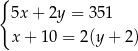 D)
D) 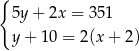
Klient banku wypłacił z bankomatu kwotę 1680 zł. Bankomat wydał kwotę w banknotach o nominałach 20 zł, 50 zł oraz 100 zł. Banknotów 100–złotowych było o 50% więcej niż 50–złotowych, a banknotów 20–złotowych było o 50% mniej niż 50–złotowych. Niech  oznacza liczbę banknotów 50–złotowych, a
oznacza liczbę banknotów 50–złotowych, a 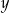 – liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb
– liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb  i
i 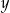 to
to
A) 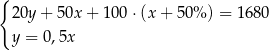 B)
B) 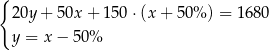
C) 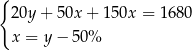 D)
D) 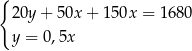
Liczba rozwiązań równania 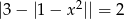 jest równa
jest równa
A) 6 B) 4 C) 2 D) 5
Rozwiązaniem równania 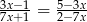 jest
jest
A) 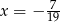 B)
B) 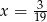 C)
C) 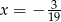 D)
D) 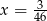
Rozwiązaniem równania 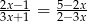 jest
jest
A) 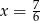 B)
B) 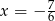 C)
C) 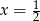 D)
D) 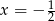
Iloczyn pierwiastków równania 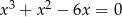 jest równy
jest równy
A) 1 B) 3 C) 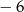 D) 0
D) 0
Liczby 7 i 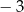 są pierwiastkami równania
są pierwiastkami równania
A) 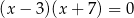 B)
B) 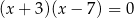
C) 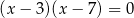 D)
D) 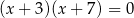
Liczby -5 i 3 są pierwiastkami równania
A) 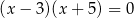 B)
B) 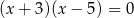
C) 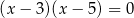 D)
D) 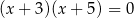
Liczby -2 i -3 są pierwiastkami równania
A)  B)
B) 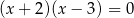
C) 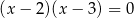 D)
D) 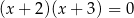
Równanie 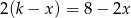 z niewiadomą
z niewiadomą  ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 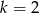 B)
B) 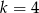 C)
C) 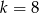 D)
D) 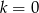
Równanie 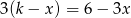 z niewiadomą
z niewiadomą  ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 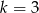 B)
B) 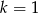 C)
C) 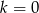 D)
D) 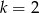
Liczby 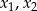 są rozwiązaniami równania
są rozwiązaniami równania 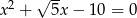 . Liczba
. Liczba 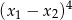 jest równa
jest równa
A) 45 B) 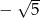 C) 2025 D) 10
C) 2025 D) 10
Rozwiązaniem równania 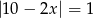 są liczby
są liczby
A) przeciwne B) różniące się o 1 C) całkowite D) niewymierne
Rozwiązaniem równania 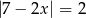 są liczby
są liczby
A) przeciwne B) różniące się o 1 C) całkowite D) różniące się o 2
Rozwiązaniem równania 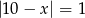 są liczby
są liczby
A) przeciwne B) różniące się o 1 C) całkowite D) niewymierne
Odwrotność liczby będącej rozwiązaniem równania 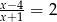 jest równa
jest równa
A) 6 B) 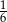 C)
C) 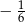 D)
D) 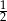
Odwrotność liczby będącej rozwiązaniem równania 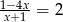 jest równa
jest równa
A) -6 B) 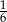 C)
C) 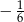 D)
D) 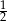
Liczba przeciwna do liczby będącej rozwiązaniem równania 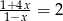 jest równa
jest równa
A) 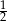 B)
B) 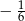 C)
C)  D) 6
D) 6

