Jednym z pierwiastków równania 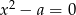 , gdzie
, gdzie  jest liczbą dodatnią, jest liczba
jest liczbą dodatnią, jest liczba 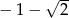 . Zatem drugim pierwiastkiem tego równania jest liczba:
. Zatem drugim pierwiastkiem tego równania jest liczba:
A) 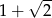 B)
B) 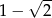 C)
C) 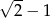 D)
D) 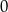
/Szkoła średnia/Zadania testowe/Równania
Funkcja 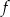 jest określona wzorem
jest określona wzorem 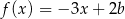 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Funkcje
. Funkcje 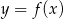 i
i 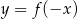 mają to samo miejsce zerowe. Wtedy
mają to samo miejsce zerowe. Wtedy
A) 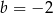 B)
B) 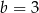 C)
C) 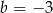 D)
D) 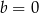
Rozwiązaniem układu równań 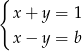 z niewiadomymi
z niewiadomymi  i
i 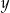 jest para liczb dodatnich. Wynika stąd, że
jest para liczb dodatnich. Wynika stąd, że
A) 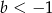 B)
B) 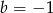 C)
C) 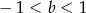 D)
D) 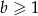
Rozwiązaniem układu równań 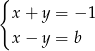 z niewiadomymi
z niewiadomymi  i
i 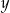 jest para liczb ujemnych. Wynika stąd, że
jest para liczb ujemnych. Wynika stąd, że
A) 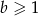 B)
B) 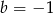 C)
C) 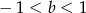 D)
D) 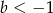
Liczby 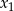 i
i 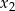 są pierwiastkami równania
są pierwiastkami równania 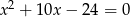 i
i 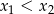 . Oblicz
. Oblicz 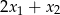 .
.
A) -22 B) -17 C) 8 D) 13
Liczby 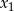 i
i 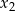 są pierwiastkami równania
są pierwiastkami równania 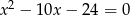 i
i 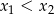 . Oblicz
. Oblicz 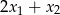 .
.
A) -22 B) -17 C) 8 D) 13
Funkcja kwadratowa jest określona wzorem 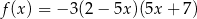 . Liczby
. Liczby 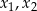 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 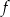 . Zatem
. Zatem
A) 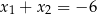 B)
B) 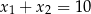 C)
C) 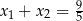 D)
D) 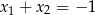
Liczba ujemnych pierwiastków równania 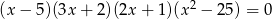 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba ujemnych pierwiastków równania 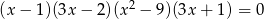 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba ujemnych pierwiastków równania 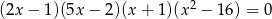 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Funkcja 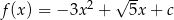 ma jedno miejsce zerowe. Zatem
ma jedno miejsce zerowe. Zatem
A) 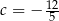 B)
B) 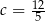 C)
C) 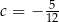 D)
D) 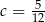
Funkcja kwadratowa 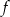 określona wzorem
określona wzorem 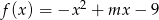 ma jedno miejsce zerowe. Zatem
ma jedno miejsce zerowe. Zatem
A) 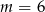 B)
B) 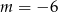 C)
C) 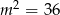 D)
D) 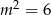
Równanie 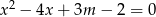 dokładnie jedno rozwiązanie gdy
dokładnie jedno rozwiązanie gdy
A) 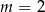 B)
B) 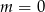 C)
C) 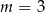 D)
D) 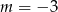
Liczby rzeczywiste 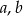 spełniają warunki:
spełniają warunki: 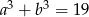 ,
, 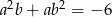 . Wtedy suma
. Wtedy suma 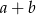 jest równa
jest równa
A) 37 B) 13 C) 1 D) 25
Jeżeli 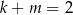 i
i 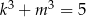 , to wartość iloczynu
, to wartość iloczynu 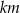 jest równa
jest równa
A)  B)
B) 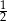 C)
C)  D)
D) 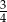
Rozwiązaniem równania 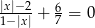 są liczby
są liczby
A) 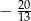 i
i 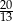 B)
B) 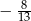 i
i 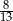 C) -8 i 8 D) -20 i 20
C) -8 i 8 D) -20 i 20
Liczba pierwiastków wielomianu 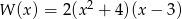 jest równa
jest równa
A) 4 B) 3 C) 2 D) 1
Liczba pierwiastków rzeczywistych wielomianu 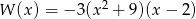 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba rozwiązań równania 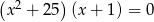 to
to
A) 3 B) 2 C) 1 D) 0
Zbiór rozwiązań równania 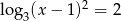 jest taki sam, jak zbiór rozwiązań równania:
jest taki sam, jak zbiór rozwiązań równania:
A) 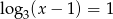 B)
B) 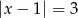 C)
C) 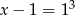 D)
D) 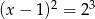
Zbiór rozwiązań równania 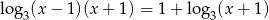 jest taki sam, jak zbiór rozwiązań równania:
jest taki sam, jak zbiór rozwiązań równania:
A) 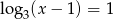 B)
B) 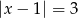 C)
C) 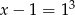 D)
D) 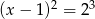
Suma wszystkich rozwiązań równania 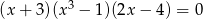 jest równa
jest równa
A) 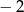 B)
B) 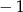 C) 0 D) 2
C) 0 D) 2
Iloczyn wszystkich rozwiązań równania 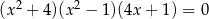 jest równy
jest równy
A) 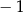 B)
B) 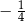 C)
C) 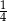 D) 1
D) 1
Rozwiązaniem równania 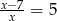 , gdzie
, gdzie 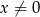 , jest liczba należąca do przedziału
, jest liczba należąca do przedziału
A) 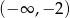 B)
B) 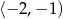 C)
C) 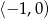 D)
D) 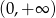
Rozwiązaniem równania 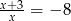 , gdzie
, gdzie 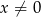 , jest liczba należąca do przedziału
, jest liczba należąca do przedziału
A) 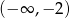 B)
B) 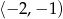 C)
C) 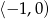 D)
D) 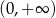
Rozwiązaniem równania 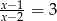 , gdzie
, gdzie  jest liczba należąca do przedziału
jest liczba należąca do przedziału
A) 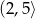 B)
B) 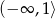 C)
C) 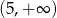 D)
D) 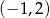
Rozwiązaniem równania 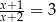 , gdzie
, gdzie 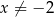 jest liczba należąca do przedziału
jest liczba należąca do przedziału
A) 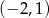 B)
B) 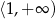 C)
C) 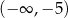 D)
D) 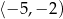
Ile rozwiązań ma układ równań 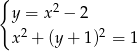 ?
?
A) 0 B) 1 C) 2 D) 3
Równanie wymierne 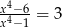 , gdzie
, gdzie 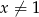 i
i 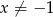 ,
,
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma dokładnie cztery rozwiązania rzeczywiste.
Dany jest wielomian 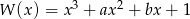 , gdzie
, gdzie  i
i 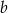 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Równanie 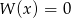 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.
B) Jeżeli równanie 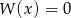 ma pierwiastek całkowity, to
ma pierwiastek całkowity, to 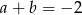 .
.
C) Jeżeli równanie 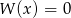 ma ujemny pierwiastek wymierny, to
ma ujemny pierwiastek wymierny, to 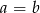 .
.
D) Równanie 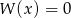 może nie mieć rozwiązań.
może nie mieć rozwiązań.
Dany jest wielomian 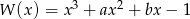 , gdzie
, gdzie  i
i 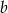 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Jeżeli równanie 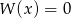 ma pierwiastek wymierny, to
ma pierwiastek wymierny, to 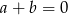 .
.
B) Jeżeli równanie 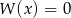 ma ujemny pierwiastek całkowity, to
ma ujemny pierwiastek całkowity, to 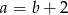 .
.
C) Równanie 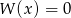 może nie mieć rozwiązań.
może nie mieć rozwiązań.
D) Równanie 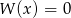 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.
Dany jest wielomian 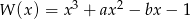 , gdzie
, gdzie  i
i 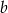 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Jeżeli równanie 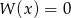 ma pierwiastek wymierny, to
ma pierwiastek wymierny, to 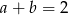 .
.
B) Jeżeli równanie 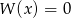 ma dodatni pierwiastek całkowity, to
ma dodatni pierwiastek całkowity, to 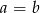 .
.
C) Równanie 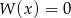 może nie mieć rozwiązań.
może nie mieć rozwiązań.
D) Równanie 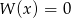 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.
Liczba 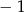 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 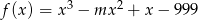 . Zatem
. Zatem
A) 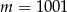 B)
B) 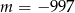 C)
C) 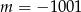 D)
D) 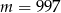
Liczba 5 jest pierwiastkiem wielomianu 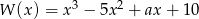 . Współczynnik
. Współczynnik  jest równy
jest równy
A) 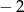 B)
B) 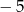 C) 2 D) 5
C) 2 D) 5
Liczba 2 jest pierwiastkiem wielomianu 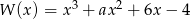 . Współczynnik
. Współczynnik  jest równy
jest równy
A) 2 B) -2 C) 4 D) -4
Liczba 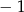 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 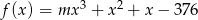 . Zatem
. Zatem
A) 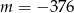 B)
B) 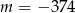 C)
C) 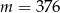 D)
D) 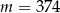
Funkcja 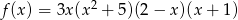 ma dokładnie
ma dokładnie
A) 1 pierwiastek B) 2 pierwiastki C) 3 pierwiastki D) 4 pierwiastki
Funkcja 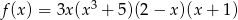 ma dokładnie
ma dokładnie
A) 1 pierwiastek B) 2 pierwiastki C) 3 pierwiastki D) 4 pierwiastki
Ile rozwiązań ma układ równań 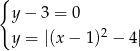
A) 1 B) 2 C) 3 D) 4
Miejscami zerowymi funkcji kwadratowej 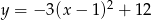 są
są
A) 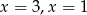 B)
B) 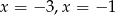 C)
C) 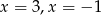 D)
D) 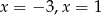
Miejscami zerowymi funkcji kwadratowej 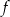 określonej wzorem
określonej wzorem 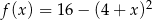 są liczby
są liczby
A) 0 oraz 4 B) 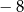 oraz 8 C) 0 oraz
oraz 8 C) 0 oraz 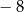 D)
D) 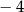 oraz 4
oraz 4
Miejscami zerowymi funkcji kwadratowej 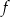 określonej wzorem
określonej wzorem 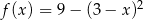 są liczby
są liczby
A) 0 oraz 3 B) 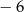 oraz 6 C) 0 oraz
oraz 6 C) 0 oraz 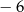 D) 0 oraz 6
D) 0 oraz 6

