/Szkoła średnia/Zadania testowe/Równania

Zadanie nr 2930724

Dodaj do ulubionych
Dodaj do rozwiązanych

Wśród miejsc zerowych wielomianu są liczby 0, 1, 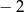− 2 . Wielomian może mieć postać:
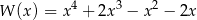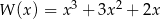
A) W (x ) = x4 + 2x3 − x2 − 2x B) W (x) = x3 + 3x2 + 2x
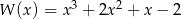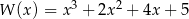
C) 3 2 W (x ) = x + 2x + x − 2 D) 3 2 W (x) = x + 2x + 4x + 5

Rozwiązanie

Sposób I

Jeżeli pierwiastkiem wielomianu jest 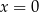x = 0 , to nie może on zawierać wyrazu wolnego, więc pozostają odpowiedzi:

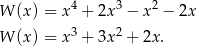
4 3 2 W (x) = x + 2x − x − 2x W (x) = x3 + 3x2 + 2x .

Łatwo teraz sprawdzić, że 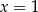x = 1 jest pierwiastkiem tylko pierwszego z nich.

Sposób II

Jeżeli liczby 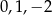0 ,1,− 2 są pierwiastkami wielomianu, to musi on być wielokrotnością wielomianu:

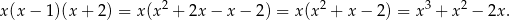
2 2 3 2 x(x − 1)(x + 2) = x(x + 2x − x − 2) = x (x + x− 2) = x + x − 2x.

Żaden z podanych wielomianów stopnia 3 nie jest wielokrotnością powyższego wielomianu, więc poprawną odpowiedzią musi być wielomian stopnia 4:

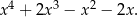
4 3 2 x + 2x − x − 2x.

 
Odpowiedź: A

Wersja PDF