/Szkoła średnia/Zadania testowe/Równania

Zadanie nr 8790688

Dodaj do ulubionych
Dodaj do rozwiązanych

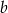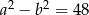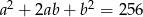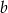Dla pewnych liczb a i b zachodzą równości: 2 2 a − b = 48 i 2 2 a + 2ab + b = 2 56 . Dla tych liczb a i b wartość wyrażenia 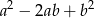a2 − 2ab + b2 jest równa
A) 9 B) 3 C) 18 D) 208

Rozwiązanie

Wiemy, że

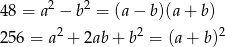
2 2 48 = a − b = (a − b)(a + b) 256 = a2 + 2ab + b2 = (a + b)2

Mamy natomiast obliczyć

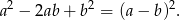
a2 − 2ab + b2 = (a− b)2.

Sposób I

Liczymy

2 (a−--b)2(a+-b-)2 [(a−--b)(a+--b)]2 482- (a − b) = (a+ b )2 = (a + b)2 = 256 = 9.

Sposób II

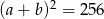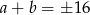Jeżeli 2 (a+ b) = 256 to a+ b = ± 16 . Wtedy z równości

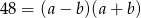
48 = (a− b)(a+ b)

mamy 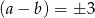(a− b) = ± 3 . Zatem 2 (a − b) = 9 .  
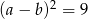Odpowiedź: A

Wersja PDF