/Szkoła średnia/Zadania testowe/Równania

Zadanie nr 9490878

Dodaj do ulubionych
Dodaj do rozwiązanych

Funkcja kwadratowa określona jest wzorem 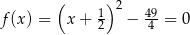( )2 f (x) = x+ 12 − 494 = 0 . Liczby 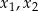x ,x 1 2 są różnymi miejscami zerowymi funkcji 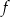f . Zatem
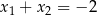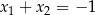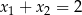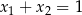
A) x1 + x2 = −2 B) x1 + x2 = − 1 C) x1 + x2 = 2 D) x1 + x2 = 1

Rozwiązanie

Sposób I

Rozwiązujemy dane równanie.

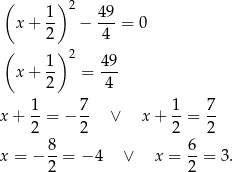
( )2 x + 1- − 49- = 0 2 4 ( )2 x + 1- = 49- 2 4 1 7 1 7 x + --= − -- ∨ x + --= -- 2 2 2 2 x = − 8-= − 4 ∨ x = 6-= 3 . 2 2

Stąd

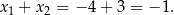
x1 + x2 = − 4 + 3 = − 1.

Sposób II

Rozwiązujemy dane równanie.

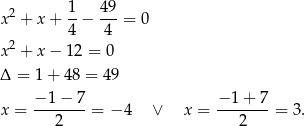
1 49 x2 + x + --− ---= 0 2 4 4 x + x − 12 = 0 Δ = 1+ 48 = 49 x = −-1−-7-= − 4 ∨ x = −-1+--7 = 3. 2 2

Stąd

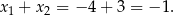
x1 + x2 = − 4 + 3 = − 1.

 
Odpowiedź: B

Wersja PDF