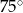Punkt 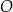 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 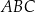 oraz
oraz 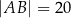 ,
, 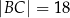 . Prosta
. Prosta 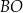 przecina bok
przecina bok 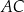 trójkąta
trójkąta 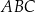 w punkcie
w punkcie 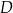 (zobacz rysunek).
(zobacz rysunek).

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 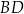 i i 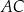 są prostopadłe. są prostopadłe. | P | F |
Stosunek pól trójkątów 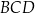 i i 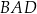 jest równy 0,9. jest równy 0,9. | P | F |

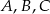 i
i 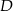 leżą na okręgu o środku
leżą na okręgu o środku 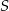 . Cięciwa
. Cięciwa 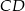 przecina średnicę
przecina średnicę 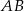 tego okręgu w punkcie
tego okręgu w punkcie 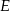 tak, że
tak, że 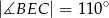 . Kąt środkowy
. Kąt środkowy 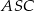 ma miarę
ma miarę 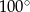 (zobacz rysunek).
(zobacz rysunek). 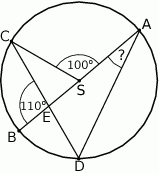
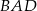 ma miarę
ma miarę 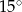
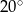
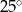
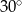
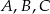 i
i 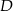 leżą na okręgu o środku
leżą na okręgu o środku 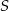 . Cięciwa
. Cięciwa 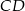 przecina średnicę
przecina średnicę 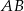 tego okręgu w punkcie
tego okręgu w punkcie 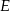 tak, że
tak, że 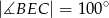 . Kąt środkowy
. Kąt środkowy 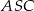 ma miarę
ma miarę 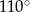 (zobacz rysunek).
(zobacz rysunek). 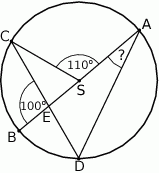
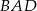 ma miarę
ma miarę 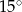
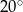
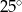
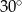
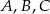 i
i 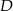 leżą na okręgu o środku
leżą na okręgu o środku 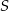 . Cięciwa
. Cięciwa 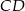 przecina średnicę
przecina średnicę 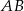 tego okręgu w punkcie
tego okręgu w punkcie 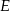 tak, że
tak, że 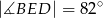 . Kąt środkowy
. Kąt środkowy 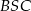 ma miarę
ma miarę 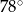 (zobacz rysunek).
(zobacz rysunek). 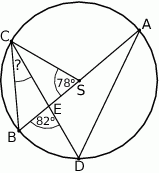
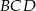 ma miarę
ma miarę 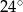
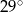
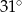
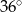
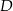 i
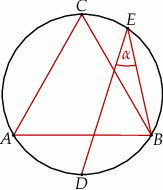
i 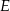 leżą na okręgu opisanym na trójkącie równobocznym
leżą na okręgu opisanym na trójkącie równobocznym 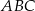 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 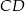 jest średnicą tego okręgu. Kąt wpisany
jest średnicą tego okręgu. Kąt wpisany 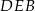 ma miarę
ma miarę  .
. 
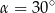
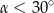
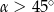
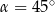
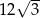 . Bok tego sześciokąta ma długość
. Bok tego sześciokąta ma długość 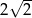
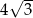
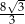 . Obwód tego sześciokąta jest równy
. Obwód tego sześciokąta jest równy 
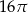 (mniejszy okrąg jest styczny do boków kwadratu
(mniejszy okrąg jest styczny do boków kwadratu 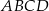 , a do większego okręgu należą punkty
, a do większego okręgu należą punkty 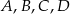 ). Zatem długość boku kwadratu
). Zatem długość boku kwadratu 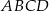 jest równa:
jest równa: 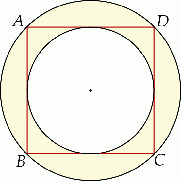
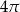 (mniejszy okrąg jest wpisany w trójkąt
(mniejszy okrąg jest wpisany w trójkąt 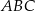 , a wierzchołki
, a wierzchołki 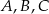 leżą na większym okręgu). Zatem długość boku trójkąta równobocznego
leżą na większym okręgu). Zatem długość boku trójkąta równobocznego  jest równa:
jest równa: 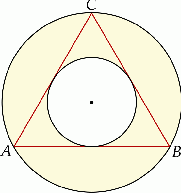
 bok
bok  ma długość 13, a wysokość
ma długość 13, a wysokość 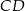 tego trójkąta dzieli bok
tego trójkąta dzieli bok 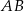 na odcinki o długościach
na odcinki o długościach 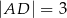 i
i 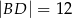 (zobacz rysunek obok).
(zobacz rysunek obok). 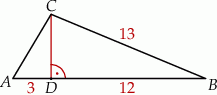
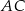 jest równa
jest równa 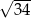
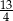
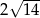
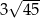
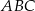 bok
bok 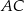 ma długość 10, a wysokość
ma długość 10, a wysokość 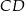 tego trójkąta dzieli bok
tego trójkąta dzieli bok 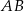 na odcinki o długościach
na odcinki o długościach 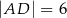 i
i 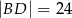 (zobacz rysunek obok).
(zobacz rysunek obok). 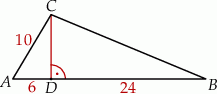
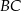 jest równa
jest równa 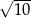
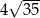
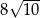
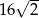
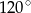 . Obwód trapezu jest równy
. Obwód trapezu jest równy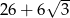
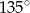 . Obwód trapezu jest równy
. Obwód trapezu jest równy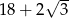
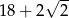
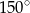 . Obwód trapezu jest równy
. Obwód trapezu jest równy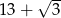
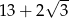
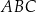 długość podstawy
długość podstawy 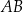 jest równa 4, a długość ramienia
jest równa 4, a długość ramienia 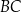 jest równa 6. Dwusieczna kąta
jest równa 6. Dwusieczna kąta 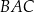 przecina bok
przecina bok 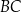 w punkcie
w punkcie 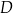 .
. 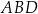 jest prostokątny.
jest prostokątny. 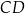 jest krótszy od odcinka
jest krótszy od odcinka 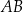 .
.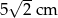
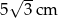
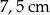
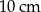
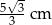 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość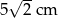
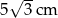
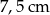
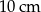
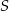 kwadratu
kwadratu 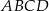 przecina proste zawierające jego boki
przecina proste zawierające jego boki 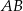 i
i 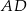 odpowiednio w punktach
odpowiednio w punktach 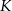 i
i 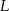 (zobacz rysunek).
(zobacz rysunek). 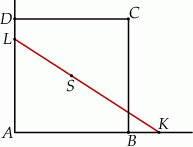
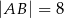 i
i 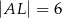 , to pole trójkąta
, to pole trójkąta 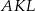 jest równe
jest równe 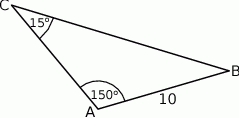
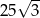
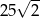
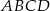 wpisany w okrąg o środku
wpisany w okrąg o środku 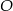 . Wówczas, jeśli
. Wówczas, jeśli 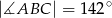 , to miara kąta
, to miara kąta 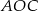 jest równa
jest równa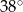
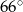
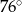
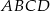 wpisany w okrąg o środku
wpisany w okrąg o środku 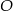 . Wówczas, jeśli
. Wówczas, jeśli 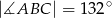 , to miara kąta
, to miara kąta 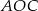 jest równa
jest równa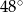
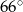
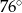
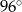
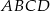 wpisany w okrąg o środku
wpisany w okrąg o środku 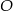 . Wówczas, jeśli
. Wówczas, jeśli 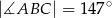 , to miara kąta
, to miara kąta 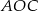 jest równa
jest równa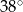
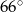
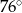
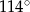
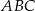 o podstawie
o podstawie 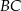 dane są:
dane są: 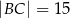 oraz
oraz 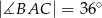 . Odcinek
. Odcinek 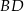 jest odcinkiem dwusiecznej kąta
jest odcinkiem dwusiecznej kąta 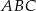 (zobacz rysunek).
(zobacz rysunek). 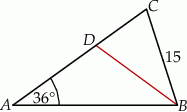
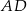 jest równa
jest równa 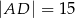
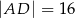
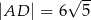
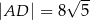
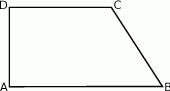
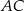 trapezu równoramiennego
trapezu równoramiennego 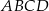 jest prostopadła do ramienia
jest prostopadła do ramienia 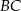 oraz tworzy z ramieniem
oraz tworzy z ramieniem 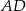 kąt ostry
kąt ostry  . Wysokość trapezu opuszczona z wierzchołka
. Wysokość trapezu opuszczona z wierzchołka 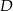 i ramię
i ramię 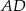 przecinają się pod kątem ostrym
przecinają się pod kątem ostrym 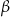 o mierze
o mierze 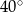 (zobacz rysunek).
(zobacz rysunek). 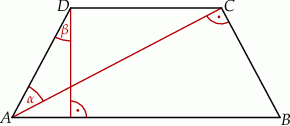
 ma miarę
ma miarę 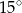
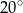
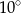
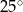
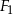 jest podobna do figury
jest podobna do figury 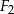 . Obwód figury
. Obwód figury 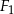 stanowi 40% obwodu
stanowi 40% obwodu 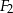 , zaś pole figury
, zaś pole figury 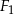 wynosi 8. Pole figury
wynosi 8. Pole figury 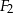 jest równe:
jest równe: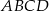 dane są
dane są 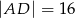 oraz
oraz 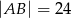 . Punkt
. Punkt 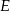 jest środkiem odcinka
jest środkiem odcinka 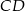 . Wówczas sinus kąta
. Wówczas sinus kąta 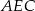 jest równy
jest równy 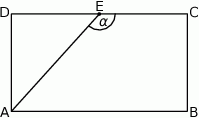


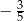
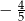
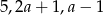 można zbudować trójkąt równoramienny. Wynika stąd, że
można zbudować trójkąt równoramienny. Wynika stąd, że 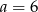
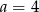
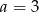
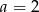
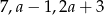 można zbudować trójkąt równoramienny. Wynika stąd, że
można zbudować trójkąt równoramienny. Wynika stąd, że 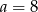
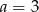
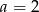
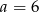
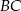 trapezu prostokątnego jest dwa razy większa od różnicy długości jego podstaw. Kąt
trapezu prostokątnego jest dwa razy większa od różnicy długości jego podstaw. Kąt 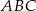 ma miarę
ma miarę 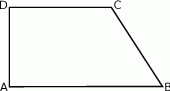
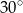
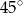
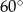
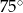
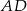 trapezu prostokątnego jest równa różnicy długości jego podstaw. Kąt
trapezu prostokątnego jest równa różnicy długości jego podstaw. Kąt 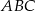 ma miarę
ma miarę