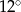Punkty 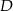 i
i 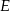 dzielą bok
dzielą bok 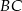 trójkąta
trójkąta 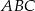 na trzy odcinki, których stosunek długości
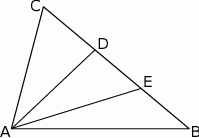
na trzy odcinki, których stosunek długości 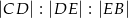 jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów
jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów 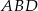 i
i 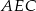 jest równy
jest równy
A)  B)
B) 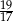 C)
C) 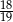 D)
D) 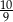
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkty 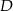 i
i 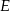 dzielą bok
dzielą bok 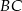 trójkąta
trójkąta 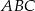 na trzy odcinki, których stosunek długości
na trzy odcinki, których stosunek długości 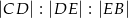 jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów
jest równy 8:9:10 (zobacz rysunek). Stosunek pól trójkątów 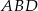 i
i 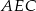 jest równy
jest równy

A)  B)
B) 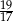 C)
C) 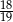 D)
D) 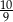
Jeżeli wysokość trójkąta równobocznego wynosi 2, to długość jego boku jest równa
A) 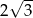 B)
B) 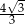 C)
C) 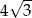 D) 6
D) 6
W trójkącie równobocznym wysokość jest równa 12. Zatem bok tego trójkąta ma długość
A) 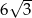 B)
B) 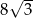 C) 24 D) 8
C) 24 D) 8
Długość boku trójkąta równobocznego o wysokości 6 cm jest równa:
A) 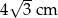 B) 12 cm C)
B) 12 cm C) 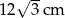 D)
D) 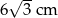
Jeżeli wysokość trójkąta równobocznego wynosi 4, to długość jego boku jest równa
A) 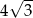 B)
B) 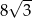 C)
C) 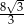 D) 12
D) 12
Jeżeli wysokość trójkąta równobocznego wynosi 3, to długość jego boku jest równa
A) 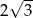 B)
B) 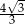 C)
C) 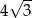 D) 6
D) 6
Jeżeli wysokość trójkąta równobocznego wynosi 6, to długość jego boku jest równa
A) 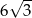 B)
B) 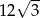 C)
C) 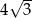 D) 18
D) 18
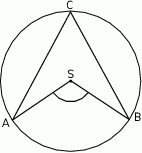
Punkt 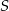 jest środkiem okręgu, na którym leżą punkty
jest środkiem okręgu, na którym leżą punkty 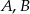 i
i 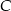 (patrz rysunek). Jeśli
(patrz rysunek). Jeśli 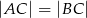 i miara kąta wypukłego
i miara kąta wypukłego 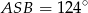 , to kąt wypukły
, to kąt wypukły 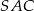 jest równy
jest równy
A) 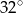 B)
B) 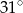 C)
C) 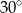 D)
D) 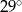
W trapezie miary kątów ostrych są równe 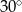 i
i 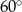 . Wówczas stosunek długości krótszego ramienia do dłuższego jest równy:
. Wówczas stosunek długości krótszego ramienia do dłuższego jest równy:
A) 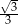 B)
B) 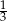 C)
C) 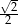 D)
D) 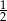
Dane są trzy okręgi o środkach 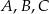 i promieniach równych odpowiednio
i promieniach równych odpowiednio 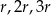 . Każde dwa z tych okręgów są zewnętrznie styczne. Jeżeli
. Każde dwa z tych okręgów są zewnętrznie styczne. Jeżeli 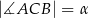 zaś
zaś 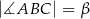 , to
, to
A) 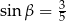 B)
B)  C)
C) 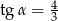 D)
D) 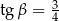
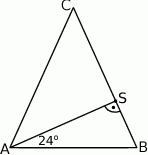
W trójkącie równoramiennym 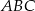 poprowadzono wysokość
poprowadzono wysokość 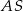 , która utworzyła z podstawą kąt o mierze
, która utworzyła z podstawą kąt o mierze 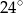 (zobacz rysunek). Ramię tego trójkąta ma długość 10. Długość wysokości
(zobacz rysunek). Ramię tego trójkąta ma długość 10. Długość wysokości 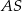 jest liczbą z przedziału
jest liczbą z przedziału
A) 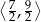 B)
B) 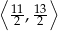 C)
C) 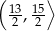 D)
D) 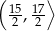
Jeśli jeden bok trójkąta ma długość 3 a drugi 5, to długość trzeciego boku nie może być równa
A) 9 B) 7 C) 6 D) 5
Długości boków trójkąta nie mogą być równe:
A) 3, 4, 4 B) 3, 4, 5 C) 3, 4, 2 D) 3, 4, 8
Jeden bok kwadratu o polu 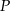 zmniejszono o 30% a drugi zwiększono o 30%. Pole powstałego w ten sposób prostokąta jest równe
zmniejszono o 30% a drugi zwiększono o 30%. Pole powstałego w ten sposób prostokąta jest równe
A) 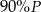 B)
B) 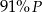 C)
C) 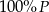 D)
D) 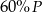
Jeden bok kwadratu wydłużono o 10%, a drugi bok skrócono o 10% w taki sposób, że otrzymano prostokąt. Pole tego prostokąta jest
A) równe polu kwadratu
B) mniejsze od pola kwadratu o 10%
C) większe od pola kwadratu o 10%
D) mniejsze od pola kwadratu o 1%
W równoległoboku 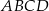 , przedstawionym na rysunku, kąt
, przedstawionym na rysunku, kąt  ma miarę
ma miarę 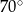 .
.
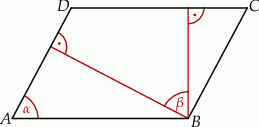
Wtedy kąt 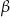 ma miarę
ma miarę
A) 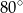 B)
B) 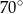 C)
C) 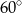 D)
D) 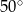
W równoległoboku 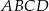 , przedstawionym na rysunku, kąt
, przedstawionym na rysunku, kąt  ma miarę
ma miarę 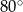 .
.
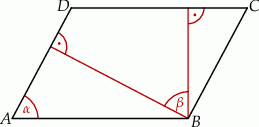
Wtedy kąt 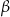 ma miarę
ma miarę
A) 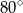 B)
B) 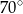 C)
C) 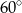 D)
D) 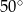
Na trójkącie 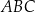 opisano okrąg i poprowadzono styczną do okręgu w punkcie
opisano okrąg i poprowadzono styczną do okręgu w punkcie 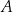 (zobacz rysunek obok).
(zobacz rysunek obok).
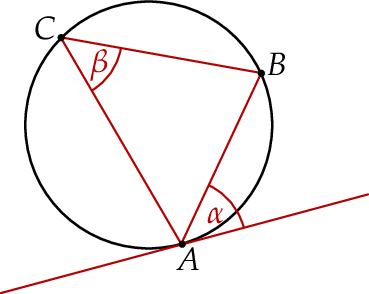
Jeżeli 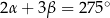 , to
, to
A) 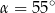 B)
B) 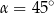 C)
C) 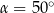 D)
D) 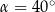
Punkt 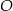 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy  ma miarę
ma miarę
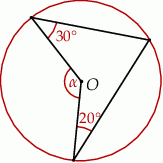
A) 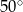 B)
B) 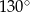 C)
C) 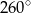 D)
D) 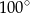
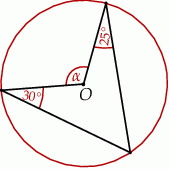
Punkt 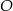 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy  ma miarę
ma miarę
A) 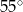 B)
B) 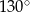 C)
C) 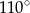 D)
D) 
Punkt 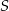 jest środkiem okręgu.
jest środkiem okręgu.
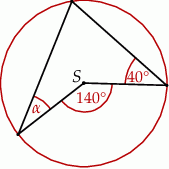
Miara kąta  wynosi
wynosi
A) 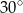 B)
B) 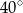 C)
C) 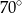 D)
D) 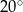
Punkt 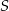 jest środkiem okręgu.
jest środkiem okręgu.
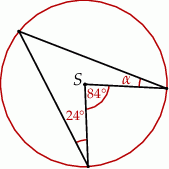
Miara kąta  wynosi
wynosi
A) 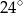 B)
B) 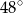 C)
C) 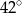 D)
D) 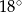
W okręgu o środku 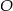 dany jest kąt wpisany
dany jest kąt wpisany 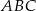 o mierze
o mierze 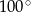
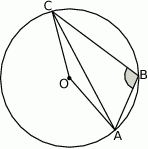
Miara kąta 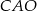 jest równa
jest równa
A) 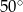 B)
B) 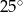 C)
C) 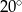 D)
D) 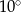
Dany jest trójkąt równoramienny 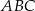 , w którym
, w którym 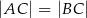 . Dwusieczna kąta poprowadzona z wierzchołka
. Dwusieczna kąta poprowadzona z wierzchołka 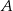 przecina bok
przecina bok 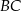 tego trójkąta w punkcie
tego trójkąta w punkcie 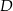 . Kąt
. Kąt 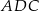 ma miarę
ma miarę 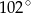 . Kąt między ramionami tego trójkąta ma miarę
. Kąt między ramionami tego trójkąta ma miarę
A) 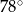 B)
B) 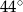 C)
C) 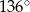 D)
D) 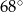
W rombie 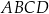 o polu
o polu 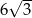 dłuższa przekątna
dłuższa przekątna 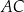 tworzy z bokiem
tworzy z bokiem 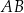 kąt o mierze
kąt o mierze 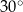 (zobacz rysunek).
(zobacz rysunek).
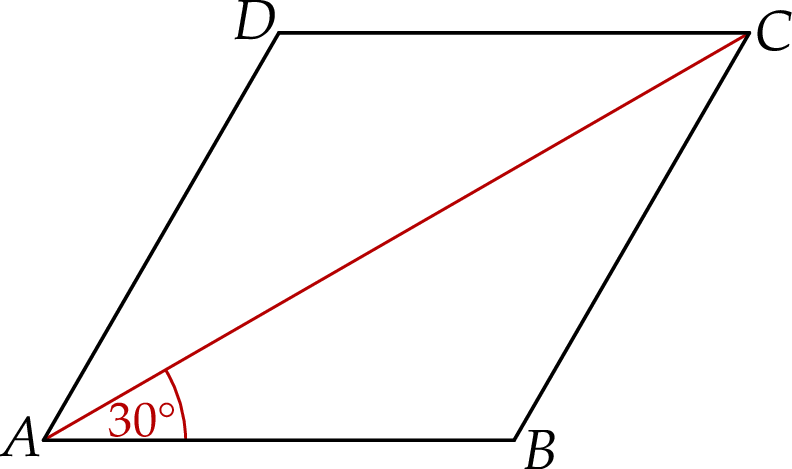
Długość przekątnej 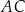 jest równa
jest równa
A) 6 B) 9 C) 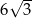 D)
D) 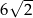
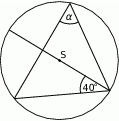
Punkt 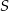 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
A) 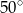 B)
B) 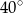 C)
C) 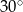 D)
D) 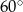
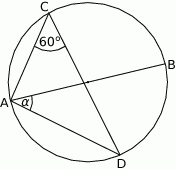
Na rysunku odcinek 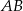 jest średnicą okręgu, a kąt
jest średnicą okręgu, a kąt 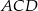 ma miarę
ma miarę 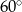 . Miara kąta
. Miara kąta 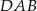 jest równa
jest równa
A) 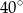 B)
B) 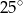 C)
C) 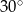 D)
D) 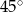
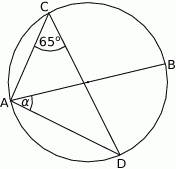
Na rysunku odcinek 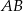 jest średnicą okręgu, a kąt
jest średnicą okręgu, a kąt 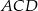 ma miarę
ma miarę 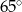 . Miara kąta
. Miara kąta 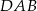 jest równa
jest równa
A) 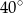 B)
B) 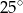 C)
C) 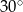 D)
D) 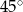
Punkty 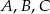 i
i 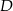 leżą na okręgu o środku
leżą na okręgu o środku 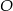 (zobacz rysunek). Miary zaznaczonych kątów
(zobacz rysunek). Miary zaznaczonych kątów  i
i 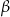 są odpowiednio równe
są odpowiednio równe
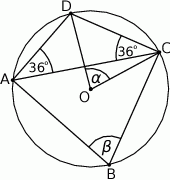
A) 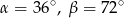 B)
B) 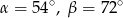 C)
C) 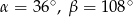 D)
D) 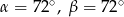
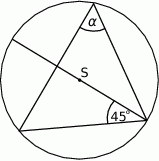
Punkt  jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
A) 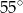 B)
B) 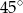 C)
C) 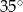 D)
D) 
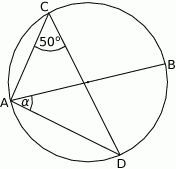
Na rysunku odcinek 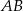 jest średnicą okręgu, a kąt
jest średnicą okręgu, a kąt 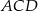 ma miarę
ma miarę 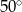 . Miara kąta
. Miara kąta 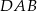 jest równa
jest równa
A) 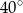 B)
B) 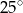 C)
C) 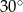 D)
D) 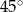
Na okręgu o środku 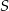 leżą punkty
leżą punkty 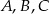 i
i 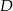 . Odcinek
. Odcinek 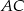 jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą
jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą 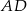 jest równy
jest równy 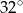 (zobacz rysunek).
(zobacz rysunek).
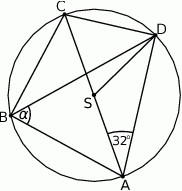
Kąt  między cięciwami
między cięciwami 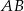 i
i 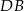 jest równy
jest równy
A) 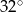 B)
B) 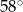 C)
C) 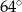 D)
D) 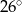
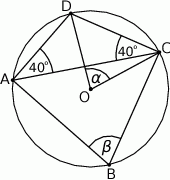
Punkty 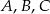 i
i 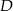 leżą na okręgu o środku
leżą na okręgu o środku 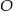 (zobacz rysunek). Miary zaznaczonych kątów
(zobacz rysunek). Miary zaznaczonych kątów  i
i 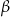 są odpowiednio równe
są odpowiednio równe
A) 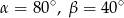 B)
B) 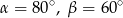 C)
C) 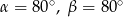 D)
D) 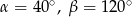
Na okręgu o środku 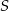 leżą punkty
leżą punkty 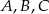 i
i 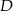 . Odcinek
. Odcinek 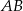 jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą
jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą 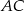 jest równy
jest równy 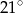 (zobacz rysunek).
(zobacz rysunek).
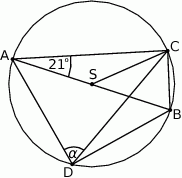
Kąt  między cięciwami
między cięciwami 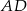 i
i 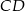 jest równy
jest równy
A) 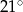 B)
B) 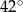 C)
C) 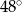 D)
D) 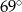
Punkt 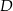 jest środkiem podstawy trójkąta równoramiennego
jest środkiem podstawy trójkąta równoramiennego 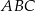 , w którym
, w którym 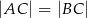 . Odległość punktu
. Odległość punktu 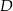 od prostej
od prostej 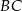 jest równa 12, a długość odcinka
jest równa 12, a długość odcinka 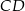 jest równa 20.
jest równa 20.
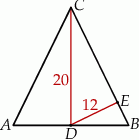
Podstawa 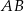 trójkąta
trójkąta 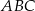 ma długość
ma długość
A) 15 B) 30 C) 24 D) 16
Odcinki 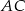 i
i 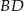 są równoległe.
są równoległe.
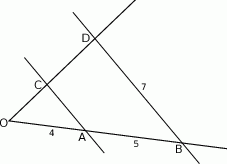
Długości odcinków podane są na rysunku. Długość odcinka 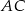 jest równa
jest równa
A) 6 B) 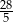 C)
C) 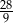 D)
D) 
Odcinki 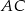 i
i 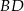 są równoległe.
są równoległe.
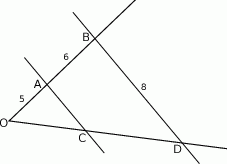
Długości odcinków podane są na rysunku. Długość odcinka 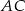 jest równa
jest równa
A) 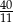 B)
B) 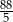 C)
C) 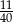 D)
D) 
Proste 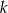 i
i 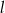 są równoległe. Odcinek
są równoległe. Odcinek  ma długość
ma długość
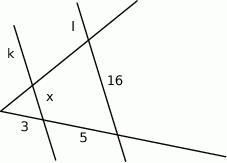
A) 9,6 B) 2 C) 6 D) 1,5
Jakim procentem koła jest pole wycinka koła zaznaczonego na rysunku?
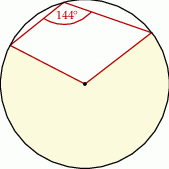
A) 92,5% B) 85% C) 80% D) 75%
Jakim procentem koła jest pole wycinka koła zaznaczonego na rysunku?
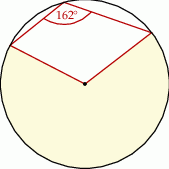
A) 90% B) 85% C) 80% D) 75%
Jakim procentem koła jest pole wycinka koła zaznaczonego na rysunku?
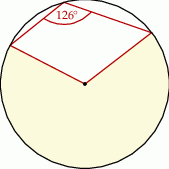
A) 90% B) 85% C) 80% D) 70%
Punkty 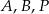 leżą na okręgu o środku
leżą na okręgu o środku 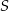 i promieniu 6. Czworokąt
i promieniu 6. Czworokąt 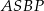 jest rombem, w którym kąt ostry
jest rombem, w którym kąt ostry 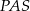 ma miarę
ma miarę 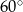 (zobacz rysunek).
(zobacz rysunek).
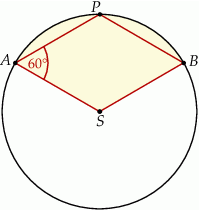
Pole zacieniowanej na rysunku figury jest równe
A) 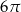 B)
B) 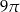 C)
C) 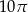 D)
D) 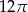
Okrąg o środku 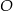 jest styczny do prostej
jest styczny do prostej 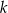 w punkcie
w punkcie 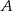 . Miara kąta
. Miara kąta  zaznaczonego na rysunku wynosi:
zaznaczonego na rysunku wynosi:
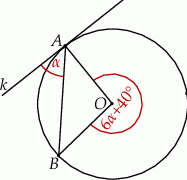
A) 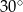 B)
B) 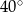 C)
C) 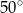 D)
D) 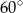
Okrąg o środku 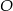 jest styczny do prostej
jest styczny do prostej 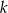 w punkcie
w punkcie 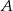 .
.
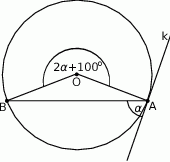
Miara kąta  zaznaczonego na rysunku wynosi
zaznaczonego na rysunku wynosi
A) 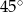 B)
B) 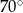 C)
C) 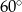 D)
D) 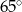
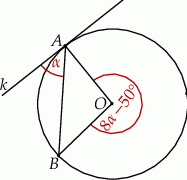
Okrąg o środku 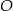 jest styczny do prostej
jest styczny do prostej 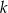 w punkcie
w punkcie 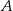 . Miara kąta
. Miara kąta  zaznaczonego na rysunku wynosi:
zaznaczonego na rysunku wynosi:
A) 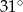 B)
B) 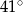 C)
C) 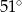 D)
D) 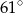
Okrąg o środku 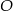 jest styczny do prostej
jest styczny do prostej 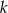 w punkcie
w punkcie 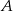 .
.
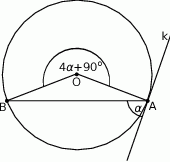
Miara kąta  zaznaczonego na rysunku wynosi
zaznaczonego na rysunku wynosi
A) 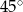 B)
B) 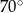 C)
C) 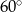 D)
D) 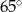
Okrąg o środku 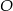 jest styczny do prostej
jest styczny do prostej 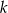 w punkcie
w punkcie 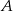 .
.
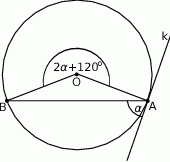
Miara kąta  zaznaczonego na rysunku wynosi
zaznaczonego na rysunku wynosi
A) 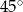 B)
B) 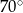 C)
C) 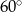 D)
D) 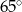
Wierzchołki trójkąta 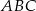 leżą na okręgu o środku
leżą na okręgu o środku 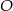 .
. 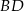 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 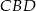 ma miarę
ma miarę 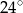 , to kąt
, to kąt 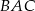 ma miarę
ma miarę
A) 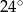 B)
B) 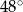 C)
C) 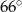 D)
D) 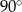
Wierzchołki trójkąta 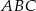 leżą na okręgu o środku
leżą na okręgu o środku 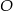 .
. 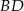 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 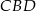 ma miarę
ma miarę 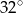 , to kąt
, to kąt 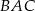 ma miarę
ma miarę
A) 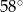 B)
B) 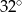 C)
C) 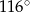 D)
D) 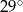
Wierzchołki trójkąta 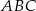 leżą na okręgu o środku
leżą na okręgu o środku 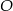 .
. 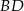 jest średnicą tego okręgu. Jeśli kąt
jest średnicą tego okręgu. Jeśli kąt 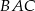 ma miarę
ma miarę 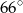 , to kąt
, to kąt 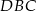 ma miarę
ma miarę
A) 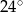 B)
B) 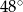 C)
C) 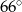 D)
D)