Obwód trójkąta 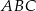 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy
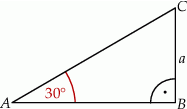
A) 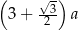 B)
B) 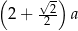 C)
C) 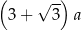 D)
D) 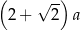
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Obwód trójkąta 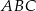 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy

A) 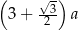 B)
B) 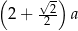 C)
C) 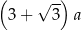 D)
D) 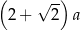
Obwód trójkąta 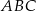 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy
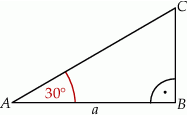
A) 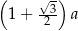 B)
B) 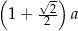 C)
C) 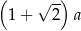 D)
D) 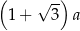
Wielokąt o polu 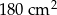 przekształcono przez podobieństwo o skali
przekształcono przez podobieństwo o skali 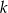 tak, że jego pole zmniejszyło się o
tak, że jego pole zmniejszyło się o 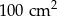 . Skala podobieństwa jest równa:
. Skala podobieństwa jest równa:
A) 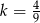 B)
B) 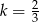 C)
C) 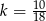 D)
D) 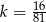
Pole trójkąta 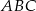 jest równe 17, a jego obwód 22. Jaki jest obwód trójkąta o polu 68, podobnego do trójkąta
jest równe 17, a jego obwód 22. Jaki jest obwód trójkąta o polu 68, podobnego do trójkąta 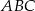 ?
?
A) 34 B) 44 C) 51 D) 88
Trójkąty 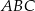 oraz
oraz 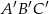 są podobne. Obwód trójkąta
są podobne. Obwód trójkąta 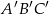 jest równy 12, a jego pole 6. Jeżeli pole trójkąta
jest równy 12, a jego pole 6. Jeżeli pole trójkąta 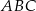 jest równe
jest równe 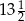 , to jego obwód wynosi
, to jego obwód wynosi
A) 18 B) 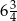 C) 27 D) 9
C) 27 D) 9
Przekątne trapezu 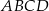 przecinają się w punkcie
przecinają się w punkcie 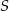 w ten sposób, że pole trójkąta
w ten sposób, że pole trójkąta 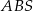 jest 4 razy większe od pola trójkąta
jest 4 razy większe od pola trójkąta 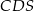 .
.
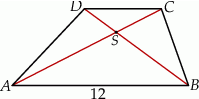
Jeżeli podstawa 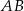 ma długość 12, to długość podstawy
ma długość 12, to długość podstawy 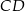 jest równa
jest równa
A) 8 B) 3 C) 6 D) 9
W równoległoboku 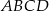 na przekątnej
na przekątnej 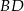 wybrano punkty
wybrano punkty 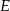 i
i 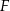 tak, że
tak, że 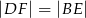 (zobacz rysunek). Dane są ponadto:
(zobacz rysunek). Dane są ponadto: 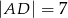 ,
, 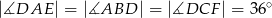 .
.
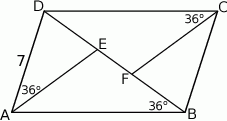
Wówczas długość odcinka 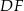 jest równa
jest równa
A) 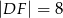 B)
B) 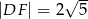 C)
C) 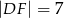 D)
D) 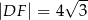
Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 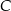 . Środkowa
. Środkowa 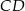 tworzy z przyprostokątną
tworzy z przyprostokątną 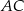 kąt
kąt 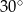 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 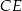 trójkąta ma miarę
trójkąta ma miarę
A) 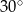 B)
B) 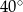 C)
C) 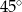 D)
D) 
Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 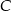 . Środkowa
. Środkowa 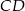 tworzy z przyprostokątną
tworzy z przyprostokątną 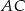 kąt
kąt 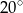 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 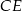 trójkąta ma miarę
trójkąta ma miarę
A) 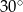 B)
B) 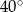 C)
C) 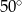 D)
D) 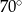
Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 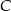 . Środkowa
. Środkowa 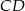 tworzy z przyprostokątną
tworzy z przyprostokątną 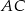 kąt
kąt 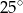 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 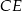 trójkąta ma miarę
trójkąta ma miarę
A) 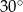 B)
B) 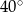 C)
C) 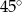 D)
D) 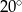
W równoległoboku o bokach 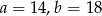 dłuższa wysokość ma długość 12. Wynika z tego, że krótsza wysokość ma długość
dłuższa wysokość ma długość 12. Wynika z tego, że krótsza wysokość ma długość
A) 14 B) 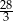 C)
C) 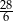 D) 5
D) 5
W równoległoboku o bokach 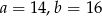 dłuższa wysokość ma długość 12. Wynika z tego, że krótsza wysokość ma długość
dłuższa wysokość ma długość 12. Wynika z tego, że krótsza wysokość ma długość
A) 21 B) 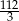 C)
C) 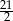 D)
D) 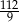
W równoległoboku 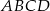 mamy dane
mamy dane 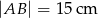 i
i 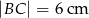 . Jedna z wysokości tego równoległoboku ma długość
. Jedna z wysokości tego równoległoboku ma długość 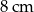 . Zatem druga wysokość ma długość
. Zatem druga wysokość ma długość
A) 20 cm B) 10 cm C) 3,2 cm D) 1,6 cm
W równoległoboku o bokach 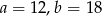 dłuższa wysokość ma długość 12. Wynika z tego, że krótsza wysokość ma długość
dłuższa wysokość ma długość 12. Wynika z tego, że krótsza wysokość ma długość
A) 8 B) 12 C) 9 D) 4
Na boku 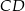 prostokąta
prostokąta 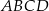 wybrano punkt
wybrano punkt 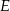 taki, że
taki, że 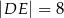 . Przekątna
. Przekątna 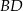 i odcinek
i odcinek 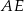 przecinają się w punkcie
przecinają się w punkcie 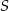 oraz
oraz 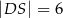 . Bok
. Bok 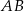 prostokąta
prostokąta 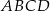 ma długość 12 (zobacz rysunek).
ma długość 12 (zobacz rysunek).
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 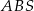 jest 5 razy mniejsze od pola prostokąta jest 5 razy mniejsze od pola prostokąta 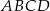 . . | P | F |
Obwód trójkąta 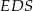 stanowi stanowi  obwodu trójkąta obwodu trójkąta 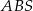 . . | P | F |
Odcinek o długości 60 cm podzielono na trzy części, których stosunek długości jest równy 3:4:5. Najdłuższa z tych części ma długość
A) 30 cm B) 12,5 cm C) 25 cm D) 15 cm
Drut o długości 45 m pocięto na trzy części, których stosunek długości jest równy 2 : 3 : 4. Najkrótsza z tych części ma długość:
A) 5 m B) 10 m C) 15 m D) 20 m
Odcinek o długości 2,4 m podzielono w stosunku 2:3:5. Najdłuższy z wyznaczonych odcinków ma długość
A) 120 cm B) 0,72 m C) 480 mm D) 14 dm
Dany jest trójkąt 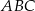 , w którym
, w którym 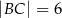 . Miara kąta
. Miara kąta 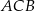 jest równa
jest równa 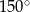 (zobacz rysunek).
(zobacz rysunek).
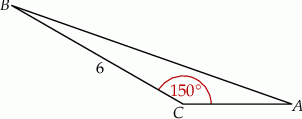
Wysokość trójkąta 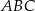 opuszczona z wierzchołka
opuszczona z wierzchołka 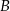 jest równa
jest równa
A) 3 B) 4 C) 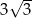 D)
D) 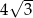
W kole poprowadzono cięciwę tworzącą ze średnicą kąt 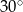 . Cięciwa dzieli średnicę na dwa odcinki o długościach 6 cm i 2 cm. Zatem odległość środka okręgu od cięciwy jest równa
. Cięciwa dzieli średnicę na dwa odcinki o długościach 6 cm i 2 cm. Zatem odległość środka okręgu od cięciwy jest równa
A) 2 cm B) 1 cm C) 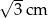 D)
D) 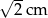
W kole poprowadzono cięciwę tworzącą ze średnicą kąt 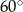 . Cięciwa dzieli średnicę na dwa odcinki o długościach 6 cm i 2 cm. Zatem odległość środka okręgu od cięciwy jest równa
. Cięciwa dzieli średnicę na dwa odcinki o długościach 6 cm i 2 cm. Zatem odległość środka okręgu od cięciwy jest równa
A) 2 cm B) 1 cm C) 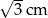 D)
D) 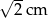
W kole poprowadzono cięciwę tworzącą ze średnicą kąt 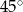 . Cięciwa dzieli średnicę na dwa odcinki o długościach 6 cm i 2 cm. Zatem odległość środka okręgu od cięciwy jest równa
. Cięciwa dzieli średnicę na dwa odcinki o długościach 6 cm i 2 cm. Zatem odległość środka okręgu od cięciwy jest równa
A) 2 cm B) 1 cm C) 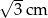 D)
D) 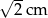
Proste 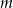 i
i  są styczne do okręgu i przecinają się pod kątem
są styczne do okręgu i przecinają się pod kątem 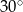 .
.
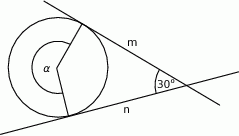
Miara kąta  jest równa
jest równa
A) 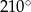 B)
B) 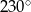 C)
C) 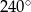 D)
D) 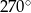
Proste 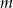 i
i  są styczne do okręgu i przecinają się pod kątem
są styczne do okręgu i przecinają się pod kątem 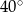 .
.
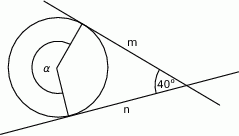
Miara kąta  jest równa
jest równa
A) 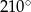 B)
B) 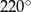 C)
C) 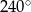 D)
D) 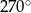
Różnica miar dwóch przeciwległych kątów deltoidu jest równa 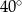 . Suma miar dwóch sąsiednich kątów tego deltoidu może być równa
. Suma miar dwóch sąsiednich kątów tego deltoidu może być równa
A) 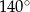 B)
B) 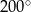 C)
C) 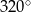 D)
D) 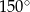
Pole sześciokąta foremnego o boku długości 6 jest równe
A) 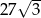 B)
B) 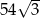 C)
C) 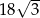 D)
D) 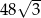
Pole sześciokąta foremnego o boku długości 4 jest równe
A) 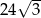 B)
B) 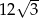 C)
C) 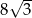 D)
D) 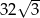
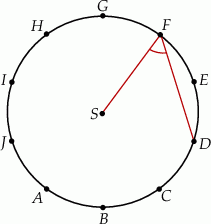
Punkty 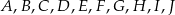 dzielą okrąg o środku
dzielą okrąg o środku 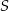 na dziesięć równych łuków. Oblicz miarę kąta
na dziesięć równych łuków. Oblicz miarę kąta 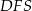 zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 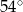 B)
B) 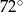 C)
C) 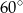 D)
D) 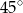
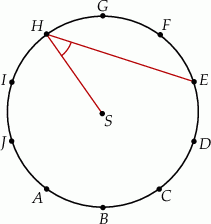
Punkty 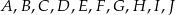 dzielą okrąg o środku
dzielą okrąg o środku  na dziesięć równych łuków. Oblicz miarę kąta
na dziesięć równych łuków. Oblicz miarę kąta 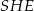 zaznaczonego na rysunku.
zaznaczonego na rysunku.
A) 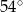 B)
B) 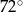 C)
C) 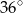 D)
D) 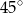
Jeden kąt trójkąta ma miarę 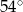 . Z pozostałych dwóch kątów tego trójkąta jeden jest 6 razy większy od drugiego. Miary pozostałych kątów są równe
. Z pozostałych dwóch kątów tego trójkąta jeden jest 6 razy większy od drugiego. Miary pozostałych kątów są równe
A) 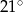 i
i 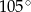 B)
B) 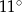 i
i 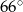 C)
C) 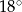 i
i 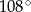 D)
D) 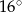 i
i 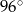
Jeden kąt trójkąta ma miarę 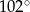 . Z pozostałych dwóch kątów tego trójkąta jeden jest 5 razy większy od drugiego. Miary pozostałych kątów są równe
. Z pozostałych dwóch kątów tego trójkąta jeden jest 5 razy większy od drugiego. Miary pozostałych kątów są równe
A) 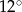 i
i 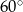 B)
B) 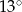 i
i 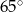 C)
C) 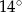 i
i 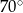 D)
D) 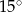 i
i 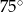
Jeden z kątów wewnętrznych trójkąta ma 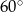 , a miary dwóch pozostałych kątów pozostają w stosunku jak 1:4. Miara kąta rozwartego tego trójkąta wynosi
, a miary dwóch pozostałych kątów pozostają w stosunku jak 1:4. Miara kąta rozwartego tego trójkąta wynosi
A) 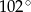 B)
B) 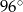 C)
C) 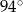 D)
D) 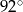
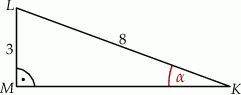
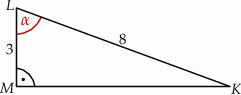
Przyprostokątna 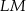 trójkąta prostokątnego
trójkąta prostokątnego 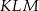 ma długość 3, a przeciwprostokątna
ma długość 3, a przeciwprostokątna 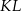 ma długość 8 (zobacz rysunek).
ma długość 8 (zobacz rysunek).
Wtedy miara  kąta ostrego
kąta ostrego 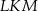 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 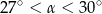 B)
B) 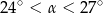 C)
C) 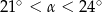 D)
D) 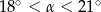
Przyprostokątna 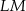 trójkąta prostokątnego
trójkąta prostokątnego 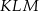 ma długość 3, a przeciwprostokątna
ma długość 3, a przeciwprostokątna 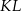 ma długość 8 (zobacz rysunek).
ma długość 8 (zobacz rysunek).
Wtedy miara  kąta ostrego
kąta ostrego 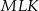 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 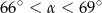 B)
B) 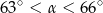 C)
C) 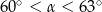 D)
D) 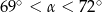
Z odcinków o długościach: 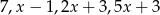 można zbudować trapez równoramienny. Wynika stąd, że
można zbudować trapez równoramienny. Wynika stąd, że
A) 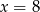 B)
B) 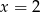 C)
C)  D)
D) 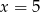
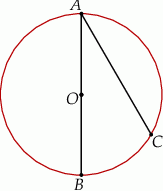
Odcinek 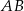 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 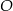 i promieniu
i promieniu  (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 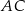 ma długość
ma długość 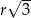 , więc
, więc
A) 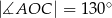 B)
B) 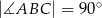 C)
C) 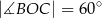 D)
D) 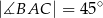
W okręgu o promieniu 6 poprowadzono cięciwę 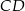 równoległą do średnicy
równoległą do średnicy 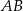 tego okręgu i taką, że
tego okręgu i taką, że 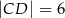 (zobacz rysunek).
(zobacz rysunek).
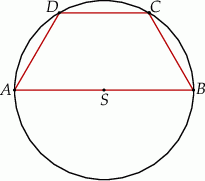
Obwód trapezu 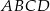 jest równy
jest równy
A) 30 B) 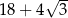 C)
C) 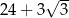 D) 32
D) 32
