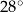Przez punkt przecięcia wysokości trójkąta równobocznego 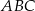 poprowadzono prostą
poprowadzono prostą 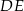 równoległą do podstawy
równoległą do podstawy 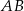 (zobacz rysunek).
(zobacz rysunek).
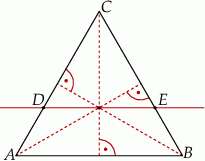
Stosunek pola trójkąta 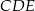 do pola trapezu
do pola trapezu 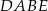 jest równy
jest równy
A) 5 : 9 B) 4 : 5 C) 4 : 9 D) 3 : 2
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Przez punkt przecięcia wysokości trójkąta równobocznego 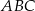 poprowadzono prostą
poprowadzono prostą 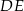 równoległą do podstawy
równoległą do podstawy 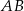 (zobacz rysunek).
(zobacz rysunek).

Stosunek pola trójkąta 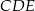 do pola trapezu
do pola trapezu 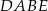 jest równy
jest równy
A) 5 : 9 B) 4 : 5 C) 4 : 9 D) 3 : 2
Wysokość rombu jest dwa razy krótsza od jego boku. Kąt rozwarty rombu ma miarę:
A) 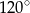 B)
B) 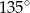 C)
C) 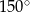 D)
D) 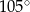
Prosta 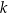 jest styczna w punkcie
jest styczna w punkcie 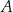 do okręgu opisanego na trójkącie równoramiennym
do okręgu opisanego na trójkącie równoramiennym 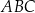 , w którym
, w którym 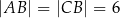 . Prosta
. Prosta 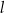 zawiera punkty
zawiera punkty 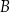 i
i 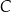 i przecina prostą
i przecina prostą 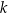 w punkcie
w punkcie 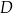 , przy czym
, przy czym 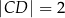 i
i 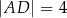 (zobacz rysunek).
(zobacz rysunek).

Długość odcinka 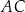 jest równa
jest równa
A) 3 B)  C)
C) 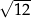 D)
D) 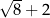
Dany jest trójkąt równoboczny 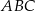 o boku długości 8. Ze środka
o boku długości 8. Ze środka 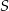 boku
boku 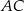 zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
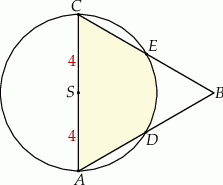
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Krótsze z łuków wyciętych przez punkty 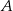 i i 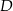 , oraz , oraz 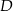 i i 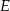 z danego okręgu, mają tą samą długość. z danego okręgu, mają tą samą długość. | P | F |
Odcinek 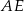 jest dwa razy dłuższy od odcinka jest dwa razy dłuższy od odcinka 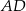 . . | P | F |
Odcinki 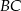 i
i 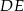 są równoległe i
są równoległe i 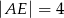 ,
, 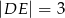 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 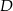 jest środkiem odcinka
jest środkiem odcinka 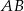 . Długość odcinka
. Długość odcinka 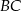 jest równa
jest równa
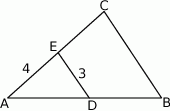
A) 4 B) 6 C) 8 D) 16
Odcinki 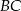 i
i 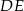 są równoległe i
są równoległe i 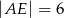 ,
, 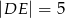 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 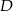 jest środkiem odcinka
jest środkiem odcinka 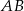 . Długość odcinka
. Długość odcinka 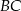 jest równa
jest równa
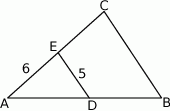
A) 10 B) 6 C) 8 D) 30
W każdym  –kącie wypukłym (
–kącie wypukłym (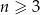 ) liczba przekątnych jest równa
) liczba przekątnych jest równa 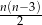 . Wielokątem wypukłym, w którym liczba przekątnych jest o 25 większa od liczby boków, jest
. Wielokątem wypukłym, w którym liczba przekątnych jest o 25 większa od liczby boków, jest
A) siedmiokąt. B) dziesięciokąt. C) dwunastokąt. D) piętnastokąt.
W każdym  –kącie wypukłym (
–kącie wypukłym (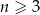 ) liczba przekątnych jest równa
) liczba przekątnych jest równa 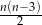 . Wielokątem wypukłym, w którym liczba przekątnych jest o 33 większa od liczby boków, jest
. Wielokątem wypukłym, w którym liczba przekątnych jest o 33 większa od liczby boków, jest
A) dziewięciokąt. B) jedenastokąt. C) dziesięciokąt. D) piętnastokąt.
Na rysunku zaznaczono punkty wspólne dwóch równoległych prostych 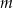 i
i  z prostymi
z prostymi 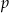 i
i 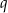 .
.
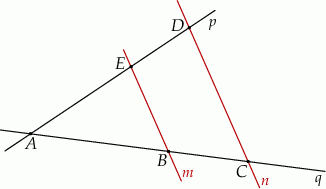
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Długości odcinków o końcach w punktach 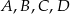 i
i 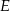 zawsze spełniają równość
zawsze spełniają równość
A) 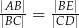 B)
B) 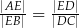 C)
C) 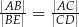
D) 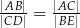 E)
E) 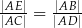 F)
F) 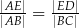
W trójkącie prostokątnym o przyprostokątnych 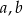 oraz przeciwprostokątnej
oraz przeciwprostokątnej  , kąt
, kąt  znajduje się naprzeciw przyprostokątnej
znajduje się naprzeciw przyprostokątnej  .
.
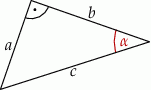
Wiadomo, że cosinus kąta  jest równy
jest równy  . Wyrażenie
. Wyrażenie 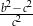 ma wartość:
ma wartość:
A) 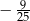 B)
B) 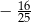 C)
C) 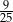 D)
D) 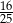
Długości boków trójkąta 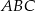 są równe 10 cm, 11 cm, 15 cm. Zatem
są równe 10 cm, 11 cm, 15 cm. Zatem
A) trójkąt ten jest ostrokątny
B) trójkąt ten jest prostokątny
C) trójkąt ten jest rozwartokątny
D) jest zbyt mało danych aby określić jakiego rodzaju jest to trójkąt
Długości boków trójkąta 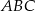 są równe 8 cm, 15 cm, 17 cm. Zatem
są równe 8 cm, 15 cm, 17 cm. Zatem
A) trójkąt ten jest ostrokątny
B) trójkąt ten jest prostokątny
C) trójkąt ten jest rozwartokątny
D) jest zbyt mało danych aby określić jakiego rodzaju jest to trójkąt
Długości boków trójkąta 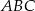 są równe 10 cm, 12 cm, 15 cm. Zatem
są równe 10 cm, 12 cm, 15 cm. Zatem
A) trójkąt ten jest ostrokątny
B) trójkąt ten jest prostokątny
C) trójkąt ten jest rozwartokątny
D) jest zbyt mało danych aby określić jakiego rodzaju jest to trójkąt
Promień koła wpisanego w trójkąt prostokątny o bokach 5 cm, 12 cm, 13 cm ma długość
A) 2,2 cm B) 1,8 cm C) 1,5 cm D) 2 cm
Promień koła wpisanego w trójkąt prostokątny o bokach 6 cm, 8 cm, 10 cm ma długość
A) 2,2 cm B) 2 cm C) 1,5 cm D) 1,8 cm
Promień koła wpisanego w trójkąt prostokątny o bokach 8 cm, 15 cm, 17 cm ma długość
A) 3 cm B) 1,8 cm C) 1,5 cm D) 2 cm
Odcinek 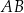 jest średnicą okręgu o środku
jest średnicą okręgu o środku 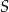 . Prosta
. Prosta 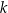 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 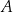 . Prosta
. Prosta 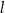 przecina ten okrąg w punktach
przecina ten okrąg w punktach 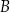 i
i 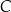 . Proste
. Proste 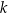 i
i 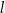 przecinają się w punkcie
przecinają się w punkcie 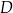 , przy czym
, przy czym 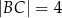 i
i 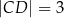 (zobacz rysunek).
(zobacz rysunek).

Odległość punktu 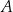 od prostej
od prostej 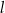 jest równa
jest równa
A) 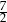 B) 5 C)
B) 5 C) 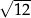 D)
D) 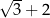
Odcinek 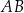 jest średnicą okręgu o środku
jest średnicą okręgu o środku 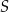 . Prosta
. Prosta 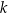 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 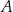 . Prosta
. Prosta 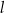 przecina ten okrąg w punktach
przecina ten okrąg w punktach 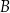 i
i 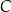 . Proste
. Proste 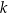 i
i 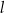 przecinają się w punkcie
przecinają się w punkcie 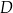 , przy czym
, przy czym 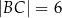 i
i 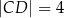 (zobacz rysunek).
(zobacz rysunek).

Odległość punktu 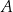 od prostej
od prostej 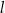 jest równa
jest równa
A) 8 B) 5 C) 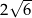 D)
D) 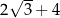
Wiedząc, że 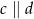 podaj miarę kąta
podaj miarę kąta  .
.
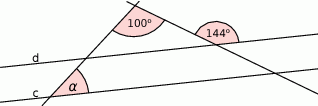
A) 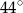 B)
B) 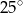 C)
C) 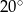 D)
D) 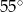
Na rysunku proste 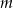 i
i  są równoległe. Kąt
są równoległe. Kąt  ma miarę
ma miarę
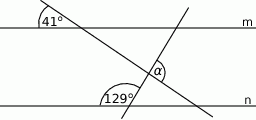
A) 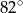 B)
B) 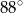 C)
C) 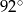 D)
D) 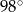
Na rysunku proste 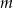 i
i  są równoległe. Kąt
są równoległe. Kąt  ma miarę
ma miarę
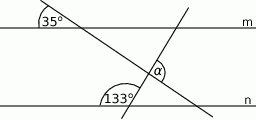
A) 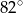 B)
B) 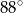 C)
C) 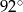 D)
D) 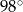
Na rysunku proste 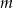 i
i  są równoległe. Kąt
są równoległe. Kąt  ma miarę
ma miarę
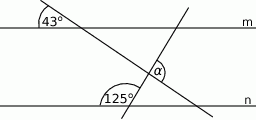
A) 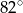 B)
B) 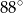 C)
C) 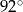 D)
D) 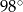
Dwusieczne kątów ostrych trójkąta prostokątnego 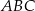 przecinają się w punkcie
przecinają się w punkcie 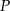 . Przyprostokątne
. Przyprostokątne 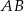 i
i 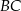 mają długości równe odpowiednio 12 i 9 (zobacz rysunek).
mają długości równe odpowiednio 12 i 9 (zobacz rysunek).
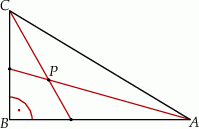
Odległość punktu 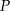 od przeciwprostokątnej
od przeciwprostokątnej 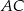 jest równa
jest równa
A) 3 B) 2 C) 15 D) 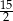
Dany jest trójkąt prostokątny 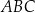 o bokach
o bokach 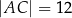 ,
, 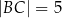 ,
, 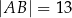 . Dwusieczne kątów tego trójkąta przecinają się w punkcie
. Dwusieczne kątów tego trójkąta przecinają się w punkcie 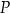 (zobacz rysunek).
(zobacz rysunek).

Odległość  punktu
punktu 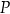 od przeciwprostokątnej
od przeciwprostokątnej 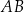 jest równa
jest równa
A) 1 B) 2 C)  D)
D) 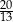
Dany jest trójkąt prostokątny 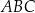 o bokach
o bokach 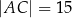 ,
, 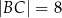 ,
, 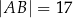 . Dwusieczne kątów tego trójkąta przecinają się w punkcie
. Dwusieczne kątów tego trójkąta przecinają się w punkcie 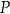 (zobacz rysunek).
(zobacz rysunek).

Odległość  punktu
punktu 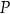 od przeciwprostokątnej
od przeciwprostokątnej 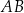 jest równa
jest równa
A) 2 B) 4 C)  D) 3
D) 3
Dany jest trójkąt prostokątny 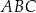 o bokach
o bokach 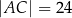 ,
, 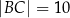 ,
, 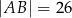 . Dwusieczne kątów tego trójkąta przecinają się w punkcie
. Dwusieczne kątów tego trójkąta przecinają się w punkcie 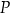 (zobacz rysunek).
(zobacz rysunek).
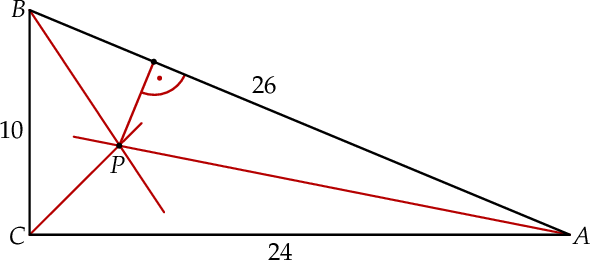
Odległość  punktu
punktu 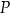 od przeciwprostokątnej
od przeciwprostokątnej 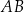 jest równa
jest równa
A) 2 B) 4 C)  D)
D) 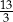
Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 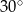 . Kąt rozwarty tego równoległoboku jest równy
. Kąt rozwarty tego równoległoboku jest równy
A) 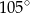 B)
B) 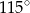 C)
C) 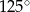 D)
D) 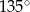
Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 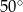 . Kąt rozwarty tego równoległoboku jest równy
. Kąt rozwarty tego równoległoboku jest równy
A) 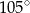 B)
B) 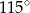 C)
C) 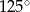 D)
D) 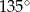
Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 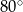 . Kąt rozwarty tego równoległoboku ma miarę
. Kąt rozwarty tego równoległoboku ma miarę
A) 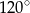 B)
B) 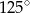 C)
C) 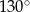 D)
D) 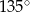
Dwa sąsiednie kąty równoległoboku różnią się o 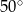 . Kąt ostry tego równoległoboku ma miarę
. Kąt ostry tego równoległoboku ma miarę
A) 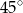 B)
B) 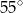 C)
C) 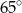 D)
D) 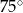
Dany jest trójkąt równoboczny 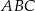 o boku długości 8. Ze środka
o boku długości 8. Ze środka 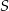 boku
boku 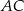 zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
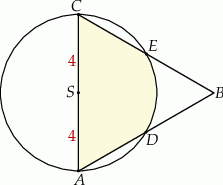
Pole powierzchni części wspólnej koła i trójkąta jest równe
A) 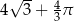 B)
B) 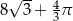 C)
C) 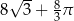 D)
D) 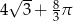
Wysokość trójkąta równobocznego jest równa 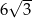 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 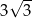 B)
B) 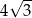 C)
C) 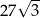 D)
D) 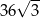
Pole trójkąta równobocznego o wysokości 3 jest równe
A) 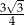 B)
B) 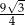 C)
C) 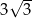 D)
D) 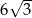
Pole rombu o boku równym 13 cm i kącie rozwartym wynoszącym 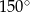 wynosi
wynosi
A) 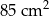 B)
B) 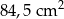 C)
C) 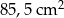 D)
D) 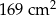
Pole rombu o obwodzie 20 i kącie rozwartym 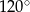 jest równe
jest równe
A) 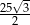 B)
B) 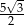 C)
C) 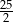 D)
D) 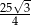
Pole rombu o boku 6 i kącie rozwartym 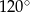 jest równe
jest równe
A) 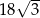 B) 18 C)
B) 18 C) 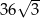 D) 36
D) 36
Pole rombu o boku 6 i kącie rozwartym 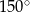 jest równe
jest równe
A) 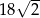 B) 18 C)
B) 18 C) 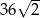 D) 36
D) 36
Pole rombu o boku równym 6 cm i kącie rozwartym wynoszącym 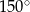 wynosi
wynosi
A) 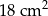 B)
B) 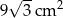 C)
C) 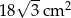 D)
D) 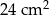
Dany jest romb o boku długości 4 i kącie rozwartym 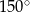 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 8 B) 12 C) 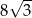 D) 16
D) 16
Trójkąt 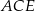 jest prostokątny oraz
jest prostokątny oraz 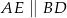 (zobacz rysunek).
(zobacz rysunek).
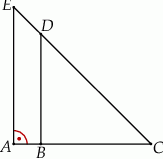
Jeżeli 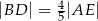 oraz
oraz 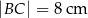 , to
, to
A) 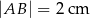 B)
B) 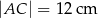 C)
C) 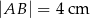 D)
D) 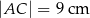
Dany jest trójkąt 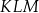 , w którym
, w którym 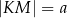 ,
, 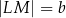 oraz
oraz 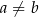 . Dwusieczna kąta
. Dwusieczna kąta 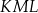 przecina bok
przecina bok 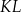 w punkcie
w punkcie 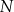 takim, że
takim, że 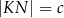 ,
, 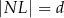 oraz
oraz 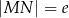 (zobacz rysunek).
(zobacz rysunek).

W trójkącie 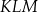 prawdziwa jest równość
prawdziwa jest równość
A) 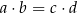 B)
B) 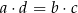 C)
C) 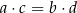 D)
D) 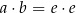
Prostokąt 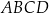 jest wpisany w okrąg. Prosta
jest wpisany w okrąg. Prosta 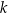 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 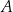 i tworzy z odcinkiem
i tworzy z odcinkiem 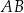 kąt o mierze
kąt o mierze  . Przekątne prostokąta
. Przekątne prostokąta 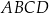 przecinają się pod kątem o mierze
przecinają się pod kątem o mierze 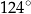 (zobacz rysunek).
(zobacz rysunek).
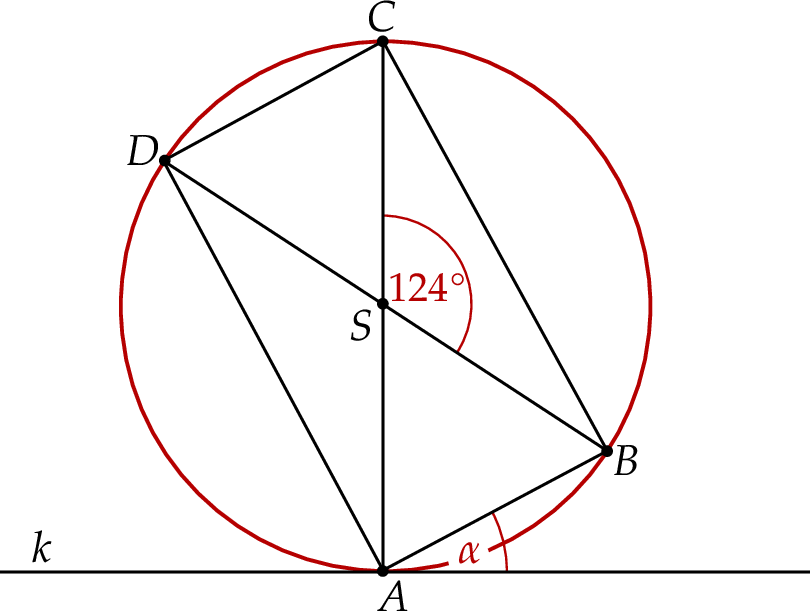
Miara kąta  jest równa
jest równa
A) 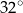 B)
B) 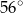 C)
C) 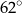 D)
D)