W trójkącie prostokątnym 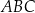 sinus kąta
sinus kąta 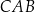 jest równy
jest równy  , a przeciwprostokątna
, a przeciwprostokątna 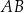 jest o 8 dłuższa od przyprostokątnej
jest o 8 dłuższa od przyprostokątnej 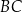 . Długość przeciwprostokątnej
. Długość przeciwprostokątnej 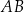 tego trójkąta jest równa
tego trójkąta jest równa
A) 18 B) 20 C) 24 D) 25
/Szkoła średnia/Zadania testowe/Geometria/Planimetria
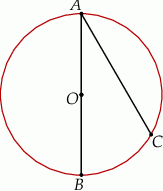
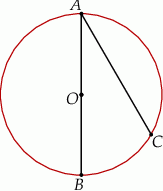
Dany jest trójkąt równoramienny 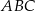 , w którym
, w którym 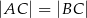 . Na podstawie
. Na podstawie 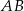 tego trójkąta leży punkt
tego trójkąta leży punkt 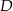 , taki że
, taki że 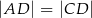 ,
, 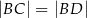 (zobacz rysunek).
(zobacz rysunek).
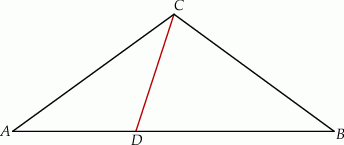
Wynika stąd, że kąt 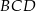 ma miarę
ma miarę
A) 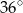 B)
B) 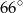 C)
C) 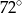 D)
D) 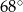
W trójkącie równoramiennym ramię ma długość 5, a kąt ostry przy podstawie jest równy  . Wysokość poprowadzona na podstawę trójkąta wynosi
. Wysokość poprowadzona na podstawę trójkąta wynosi
A) 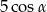 B)
B) 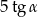 C)
C) 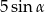 D)
D) 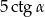
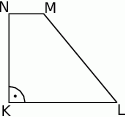
W trapezie 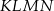 , w którym
, w którym 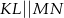 , kąt
, kąt 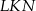 jest prosty (zobacz rysunek) oraz dane są:
jest prosty (zobacz rysunek) oraz dane są: 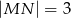 ,
, 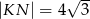 ,
, 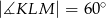 . Pole tego trapezu jest równe:
. Pole tego trapezu jest równe:
A) 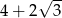 B)
B) 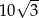 C)
C) 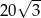 D)
D) 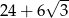
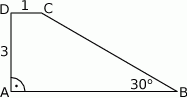
Pole trapezu prostokątnego  przedstawionego na rysunku, jest równe
przedstawionego na rysunku, jest równe
A) 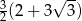 B)
B) 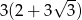 C)
C) 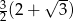 D)
D) 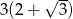
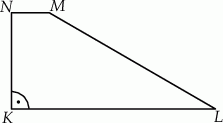
W trapezie 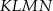 , w którym
, w którym 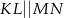 , kąt
, kąt 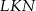 jest prosty (zobacz rysunek) oraz dane są:
jest prosty (zobacz rysunek) oraz dane są: 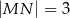 ,
, 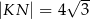 ,
, 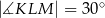 . Pole tego trapezu jest równe:
. Pole tego trapezu jest równe:
A)  B)
B) 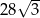 C)
C) 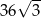 D)
D) 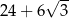
Jeżeli proste 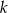 i
i 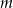 są równoległe (patrz rysunek), to długość odcinka
są równoległe (patrz rysunek), to długość odcinka  wynosi
wynosi
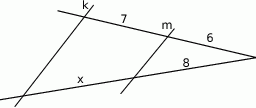
A) 9 B) 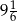 C)
C) 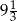 D)
D) 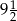
Proste 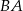 i
i 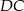 są równoległe. Długości odcinków
są równoległe. Długości odcinków 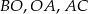 przedstawione są na rysunku. Wobec tego długość odcinka
przedstawione są na rysunku. Wobec tego długość odcinka 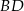 wynosi
wynosi
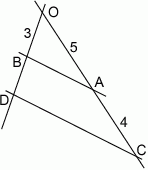
A) 10 B) 2,4 C) 5,4 D) 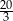
Odcinki 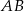 i
i 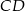 są równoległe (zobacz rysunek). Długość odcinka
są równoległe (zobacz rysunek). Długość odcinka 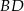 jest równa
jest równa
A)  B)
B) 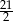 C) 3 D) 2
C) 3 D) 2
Kąt środkowy okręgu jest większy od kąta wpisanego opartego na tym samym łuku, o
A) 200% B) 150% C) 100% D) 50%
Kąt wpisany okręgu jest mniejszy od kąta środkowego opartego na tym samym łuku, o
A) 25% B) 50% C) 100% D) 150%
Przeciwprostokątna 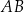 trójkąta prostokątnego
trójkąta prostokątnego 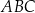 ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
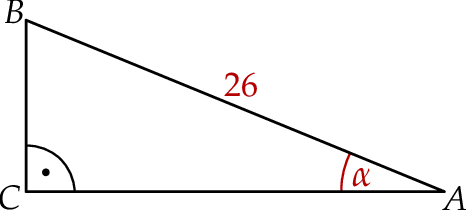
Jeżeli  jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia
jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia 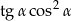 jest równa
jest równa
A) 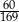 B)
B) 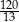 C)
C) 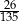 D)
D) 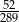
Długości boków prostokąta są równe 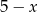 i
i 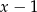 . Pole prostokąta jest największe, gdy liczba
. Pole prostokąta jest największe, gdy liczba  jest równa
jest równa
A) 2 B) 1 C) 4 D) 3
Długości boków prostokąta są równe 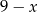 i
i 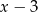 . Pole prostokąta jest największe, gdy liczba
. Pole prostokąta jest największe, gdy liczba  jest równa
jest równa
A) 7 B) 6 C) 4 D) 5
Długości boków prostokąta są równe 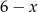 i
i 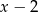 . Pole prostokąta jest największe, gdy liczba
. Pole prostokąta jest największe, gdy liczba  jest równa
jest równa
A) 2 B) 5 C) 4 D) 3
Znajdź skalę podobieństwa trójkąta 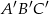 do trójkąta
do trójkąta 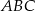 :
:
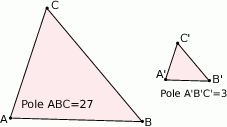
A) 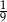 B)
B) 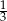 C) 3 D) 9
C) 3 D) 9
Znajdź skalę podobieństwa trójkąta 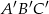 do trójkąta
do trójkąta 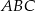 :
:
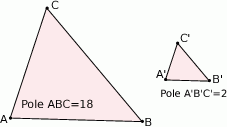
A) 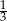 B)
B) 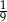 C) 3 D) 9
C) 3 D) 9
Dłuższy bok prostokąta ma długość 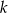 . Przekątna prostokąta tworzy z krótszym bokiem kąt
. Przekątna prostokąta tworzy z krótszym bokiem kąt  . Długość przekątnej prostokąta wynosi
. Długość przekątnej prostokąta wynosi
A) 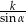 B)
B) 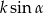 C)
C) 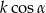 D)
D) 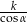
W trapezie równoramiennym kąt ostry ma miarę 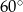 , a podstawy mają długości 12 i 6. Wysokość tego trapezu jest równa
, a podstawy mają długości 12 i 6. Wysokość tego trapezu jest równa
A) 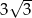 B)
B) 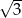 C)
C)  D)
D) 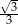
Na rysunku zaznaczono długości niektórych odcinków w rombie oraz kąt  .
.
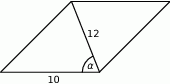
Wtedy
A) 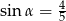 B)
B) 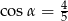 C)
C) 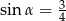 D)
D) 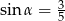
Na rysunku zaznaczono długości niektórych odcinków w rombie oraz kąt  .
.
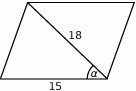
Wtedy
A) 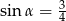 B)
B) 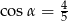 C)
C) 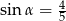 D)
D) 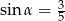
Odcinek 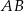 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 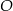 i promieniu
i promieniu 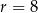 (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 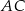 ma długość
ma długość 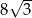 .
.
Miara kąta  jest równa
jest równa
A)  B)
B) 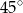 C)
C) 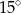 D)
D) 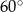
Odcinek 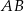 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 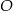 i promieniu
i promieniu 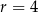 (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 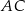 ma długość
ma długość 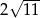 .
.
Sinus kąta 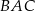 jest równy
jest równy
A) 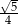 B)
B) 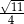 C)
C) 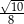 D)
D) 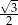
W trójkącie 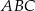 bok
bok 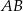 ma długość 4, a bok
ma długość 4, a bok 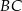 ma długość 4,6. Dwusieczna kąta
ma długość 4,6. Dwusieczna kąta 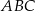 przecina bok
przecina bok 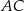 w punkcie
w punkcie 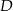 takim, że
takim, że 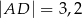 (zobacz rysunek).
(zobacz rysunek).
Odcinek  ma długość
ma długość
A) 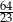 B)
B) 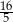 C)
C) 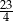 D)
D) 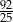
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 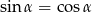 . Przeciwprostokątna tego trójkąta ma długość 2. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 2. Obwód tego trójkąta jest równy
A) 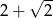 B)
B) 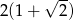 C)
C) 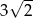 D)
D) 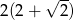
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 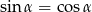 . Przeciwprostokątna tego trójkąta ma długość 6. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 6. Obwód tego trójkąta jest równy
A) 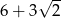 B)
B) 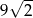 C)
C) 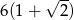 D)
D) 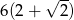
W trójkącie prostokątnym jeden z kątów ostrych jest równy  i
i 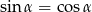 . Przeciwprostokątna tego trójkąta ma długość 5. Obwód tego trójkąta jest równy
. Przeciwprostokątna tego trójkąta ma długość 5. Obwód tego trójkąta jest równy
A) 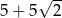 B)
B) 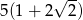 C)
C) 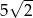 D)
D) 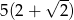
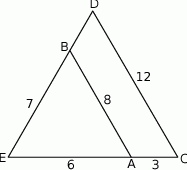
Odcinki 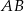 i
i 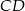 są równoległe. Długości odcinków
są równoległe. Długości odcinków 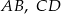 i
i  są podane na rysunku.
są podane na rysunku.
Długość odcinka 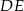 jest równa
jest równa
A) 44 B) 40 C) 36 D) 15
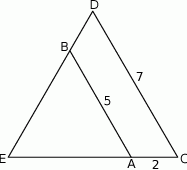
Odcinki 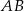 i
i 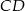 są równoległe i
są równoległe i 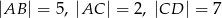 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 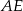 jest równa
jest równa
A) 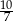 B)
B) 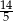 C) 3 D) 5
C) 3 D) 5
Odcinki 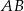 i
i 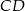 są równoległe. Długości odcinków
są równoległe. Długości odcinków 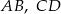 i
i 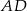 są podane na rysunku.
są podane na rysunku.
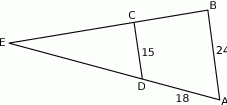
Długość odcinka 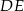 jest równa
jest równa
A) 30 B) 33 C) 27 D) 12
Odcinki 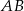 i
i 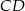 są równoległe i
są równoległe i 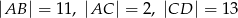 (zobacz rysunek). Długość odcinka
(zobacz rysunek). Długość odcinka 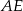 jest równa
jest równa
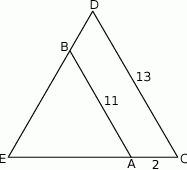
A) 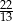 B)
B) 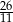 C) 11 D) 13
C) 11 D) 13
Kąt między ramionami trójkąta równoramiennego ma miarę 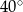 . Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
. Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
A) 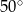 B)
B) 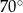 C)
C) 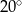 D)
D) 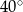
Kąt między ramionami trójkąta równoramiennego wynosi 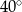 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 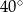 B)
B) 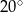 C)
C) 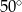 D)
D) 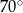
Kąt między ramionami trójkąta równoramiennego ma miarę 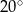 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 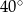 B)
B) 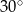 C)
C) 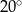 D)
D) 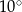
Kąt między ramionami trójkąta równoramiennego wynosi 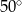 . Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
. Miara kąta nachylenia wysokości opuszczonej na ramię tego trójkąta do jego podstawy jest równa
A) 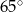 B)
B) 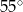 C)
C) 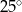 D)
D) 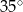
Kąt między ramionami trójkąta równoramiennego ma miarę 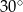 . Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
. Wysokość tego trójkąta poprowadzona do ramienia tworzy z podstawą kąt o mierze
A) 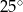 B)
B) 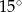 C)
C) 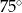 D)
D) 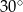
Dany jest trójkąt 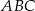 , w którym
, w którym 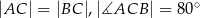 , zaś
, zaś 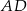 jest wysokością trójkąta. Wówczas miara kąta
jest wysokością trójkąta. Wówczas miara kąta 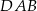 wynosi
wynosi
A) 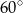 B)
B) 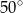 C)
C) 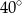 D)
D) 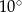
W trójkącie równobocznym 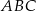 poprowadzono odcinki
poprowadzono odcinki 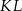 i
i 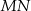 , które podzieliły boki
, które podzieliły boki 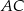 i
i 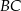 na trzy równe części. Stosunek pola trójkąta
na trzy równe części. Stosunek pola trójkąta  do pola trapezu
do pola trapezu 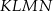 jest równy
jest równy
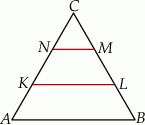
A) 3 B) 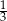 C) 9 D) 6
C) 9 D) 6
Kąt wpisany w okrąg o promieniu 10 ma miarę 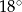 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 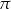 B)
B) 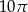 C)
C) 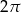 D)
D) 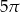
Kąt wpisany w okrąg o promieniu 9 ma miarę 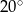 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 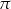 B)
B) 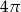 C)
C) 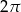 D)
D) 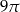
Kąt wpisany w okrąg o promieniu 9 ma miarę 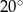 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 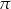 B)
B) 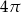 C)
C) 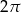 D)
D) 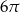
Kąt wpisany w okrąg o promieniu 8 ma miarę 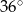 . Długość łuku, na którym oparty jest ten kąt, jest równa
. Długość łuku, na którym oparty jest ten kąt, jest równa
A) 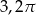 B)
B) 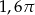 C)
C) 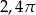 D)
D) 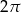
Długość odcinka  jest równa
jest równa
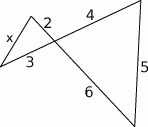
A) 1 B) 2,5 C) 2 D) 1,5
Długość odcinka 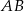 , równoległego do odcinka
, równoległego do odcinka 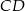 , jest równa:
, jest równa:
A) 6 B) 3 C) 2 D) 4
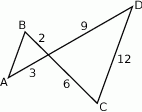
Długość odcinka  jest równa
jest równa
A) 12 B) 15 C) 10 D) 8
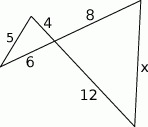
Długość odcinka  jest równa
jest równa
A) 4 B) 2 C) 3 D) 6
Długość odcinka  jest równa
jest równa
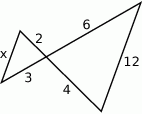
A) 6 B) 3 C) 2 D) 4
Długość odcinka  jest równa
jest równa
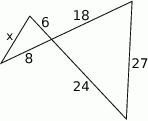
A) 9 B) 8 C) 12 D) 7,5

