Zadanie nr 3613076
Trójkąty 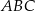 i
i 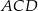 są wpisane w okrąg o środku
są wpisane w okrąg o środku 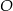 . Odcinek
. Odcinek 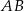 jest średnicą okręgu.
jest średnicą okręgu.
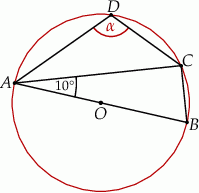
Miara kąta  zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa
A) 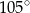 B)
B) 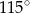 C)
C) 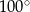 D)
D) 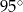
Rozwiązanie
Trójkąt 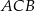 jest trójkątem opartym na średnicy, więc
jest trójkątem opartym na średnicy, więc 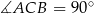 .
.
Sposób I
Czworokąt 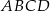 jest wpisany w okrąg, więc sumy jego przeciwległych kątów są równe
jest wpisany w okrąg, więc sumy jego przeciwległych kątów są równe 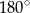 . Zatem
. Zatem
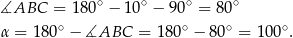
Sposób II
Dorysujmy odcinek 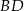 .
.
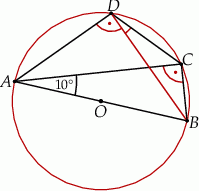
Korzystając z własności kątów wpisanych opartych na tym samym łuku mamy.
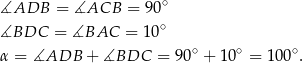
Odpowiedź: C

