Zadanie nr 3718612
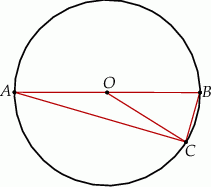
Odcinek 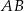 jest średnicą okręgu o środku
jest średnicą okręgu o środku 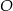 i promieniu
i promieniu  . Na tym okręgu wybrano punkt
. Na tym okręgu wybrano punkt 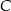 , taki, że
, taki, że 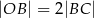 (zobacz rysunek).
(zobacz rysunek).
Pole trójkąta 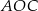 jest równe
jest równe
A) 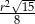 B)
B) 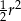 C)
C) 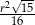 D)
D) 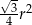
Rozwiązanie
Kąt 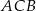 jest oparty na średnicy, więc jest prosty. Zatem
jest oparty na średnicy, więc jest prosty. Zatem
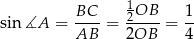
oraz
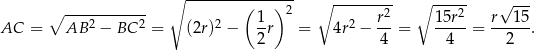
Korzystamy teraz ze wzoru z sinusem na pole trójkąta
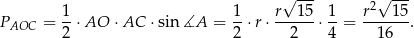
Odpowiedź: C

