Zadanie nr 4441354
W okręgu o środku w punkcie 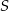 poprowadzono cięciwę
poprowadzono cięciwę 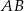 , która utworzyła z promieniem
, która utworzyła z promieniem 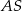 kąt o mierze
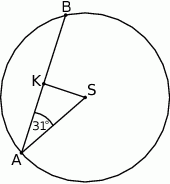
kąt o mierze 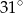 (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu
(zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu  od cięciwy
od cięciwy 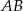 jest liczbą z przedziału
jest liczbą z przedziału
A) 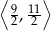 B)
B) 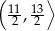 C)
C) 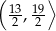 D)
D) 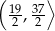
Rozwiązanie
Trójkąt 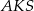 jest prostokątny, więc
jest prostokątny, więc

Sprawdzamy teraz w tablicach, że 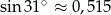 . Zatem
. Zatem
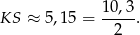
Odpowiedź: A

