Zadanie nr 4493035
Cięciwy 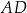 i
i 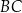 okręgu o środku
okręgu o środku 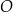 przecinają się w punkcie
przecinają się w punkcie 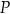 tak, że
tak, że 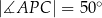 (zobacz rysunek).
(zobacz rysunek).

Jeżeli punkt 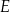 jest punktem wspólnym prostych
jest punktem wspólnym prostych 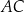 i
i 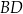 , to miara kąta
, to miara kąta 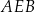 jest równa
jest równa
A) 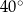 B)
B) 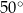 C)
C) 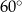 D)
D) 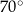
Rozwiązanie
Sposób I
Zauważmy, że każdy z kątów: 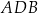 i
i 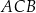 jest oparty na średnicy
jest oparty na średnicy 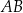 . Zatem
. Zatem
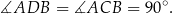
Ponadto
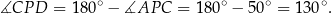
Korzystamy teraz z tego, że suma kątów w czworokącie 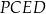 jest równa
jest równa 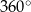 .
.
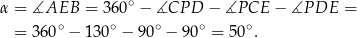
Sposób II
Tak jak poprzednio zauważamy, że
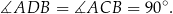
Stąd
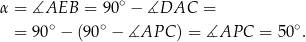
Sposób III
Tak jak poprzednio zauważamy, że
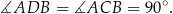
Trójkąty 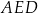 i
i 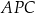 są oba prostokątne i mają wspólny kąt przy wierzchołku
są oba prostokątne i mają wspólny kąt przy wierzchołku 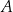 . Są więc podobne. Zatem
. Są więc podobne. Zatem
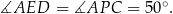
Odpowiedź: B

