/Szkoła średnia/Zadania testowe/Geometria/Planimetria

Zadanie nr 6965206

Dodaj do ulubionych
Dodaj do rozwiązanych

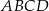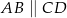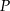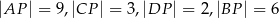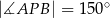Przekątne trapezu ABCD , w którym AB ∥ CD przecinają się w punkcie P w ten sposób, że |AP | = 9,|CP | = 3,|DP | = 2,|BP | = 6 oraz |∡AP B | = 150∘ . Pole tego trapezu jest równe
A) 32 B) 24 C) 18 D) 16

Rozwiązanie

Zaczynamy oczywiście od szkicowego rysunku.

PIC

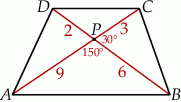
Sposób I

Korzystamy ze wzoru z długościami przekątnych na pole czworokąta.

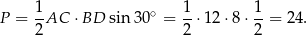
1 1 1 P = -AC ⋅BD sin 30∘ = --⋅12 ⋅8⋅ --= 24 . 2 2 2

Sposób II

Korzystamy ze wzoru na pole trójkąta z sinusem oraz z tego, że 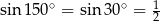sin 150∘ = sin 30∘ = 1 2 .

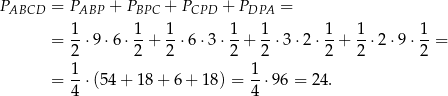
PABCD = PABP + PBPC + PCPD + PDPA = = 1-⋅9 ⋅6⋅ 1+ 1-⋅6 ⋅3⋅ 1-+ 1-⋅3 ⋅2⋅ 1-+ 1-⋅2 ⋅9 ⋅ 1-= 2 2 2 2 2 2 2 2 1- 1- = 4 ⋅(54 + 18 + 6 + 18) = 4 ⋅ 96 = 24.

 
Odpowiedź: B

Wersja PDF