/Szkoła średnia/Zadania testowe/Geometria/Planimetria

Zadanie nr 7078470

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole trójkąta prostokątnego jest równe 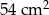2 54 cm . Różnica długości przyprostokątnych wynosi 3 cm. Jaką długość ma przeciwprostokątna tego trójkąta?
A) 14 B) 15 C) 16 D) 17

Rozwiązanie

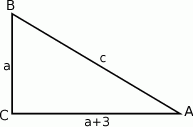
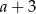Oznaczmy długości przyprostokątnych trójkąta przez a i a + 3 , a długość przeciwprostokątnej przez c .

PIC

Z podanego pola obliczamy a .

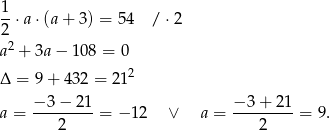
1⋅ a⋅(a + 3) = 54 / ⋅2 2 a 2 + 3a − 10 8 = 0 2 Δ = 9 + 432 = 21 − 3− 21 − 3 + 21 a = ---------= − 1 2 ∨ a = ---------= 9. 2 2

Ujemne rozwiązanie odrzucamy i mamy 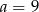a = 9 . Korzystając z twierdzenia Pitagorasa obliczamy długość przeciwprostokątnej.

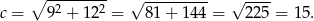
∘ -2-----2- √ --------- √ ---- c = 9 + 12 = 81 + 1 44 = 225 = 15.

 
Odpowiedź: B

Wersja PDF