Zadanie nr 7224144
W równoległoboku 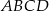 na przekątnej
na przekątnej 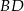 wybrano punkty
wybrano punkty 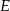 i
i 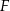 tak, że
tak, że 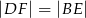 (zobacz rysunek). Dane są ponadto:
(zobacz rysunek). Dane są ponadto: 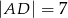 ,
, 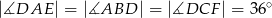 .
.
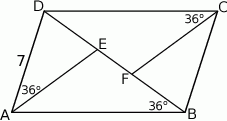
Wówczas długość odcinka 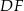 jest równa
jest równa
A) 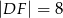 B)
B) 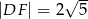 C)
C) 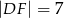 D)
D) 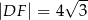
Rozwiązanie
Zauważmy, że 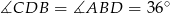 , więc trójkąt
, więc trójkąt 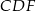 jest równoramienny. Stąd
jest równoramienny. Stąd
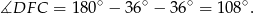
To oznacza, że trójkąty 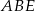 i
i 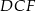 są przystające (bo mają dwa boki równej długości oraz równe kąty
są przystające (bo mają dwa boki równej długości oraz równe kąty 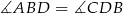 ). W takim razie
). W takim razie
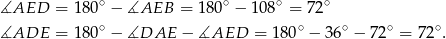
W takim razie oba trójkąty: 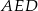 i
i 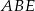 są równoramienne. Stąd
są równoramienne. Stąd
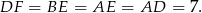
Odpowiedź: C

