Zadanie nr 7686223
W kwadracie 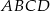 połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat 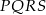 .
.
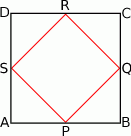
Kwadrat 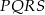 jest podobny do kwadratu
jest podobny do kwadratu 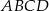 w skali
w skali
A) 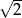 B) 2 C)
B) 2 C) 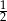 D)
D) 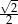
Rozwiązanie
Sposób I
Jeżeli oznaczymy bok kwadratu 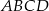 przez
przez  , to przekątna mniejszego kwadratu ma długość
, to przekątna mniejszego kwadratu ma długość  , a przekątna większego kwadratu ma długość
, a przekątna większego kwadratu ma długość 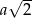 .
.
Zatem skala podobieństwa jest równa
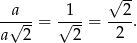
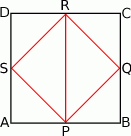
Sposób II
Zamiast patrzeć na przekątne, możemy wyliczyć długość boku mniejszego kwadratu.
Jak poprzednio, oznaczmy długość boku dużego kwadratu przez  , wtedy na mocy twierdzenia Pitagorasa w trójkącie
, wtedy na mocy twierdzenia Pitagorasa w trójkącie 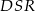 mamy
mamy
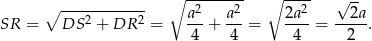
Zatem skala podobieństwa jest równa
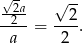
Odpowiedź: D

