Zadanie nr 7710075
Na czworokącie 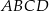 opisano okrąg o środku
opisano okrąg o środku 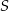 i promieniu
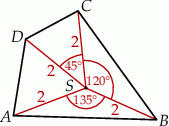
i promieniu 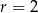 (zobacz rysunek). Pole tego czworokąta jest równe
(zobacz rysunek). Pole tego czworokąta jest równe
A) 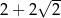 B) 4 C)
B) 4 C) 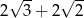 D)
D) 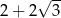
Rozwiązanie
Zauważmy najpierw, że
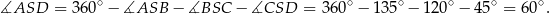
Pole czworokąta 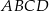 jest więc równe (korzystamy ze wzoru z sinusem)
jest więc równe (korzystamy ze wzoru z sinusem)
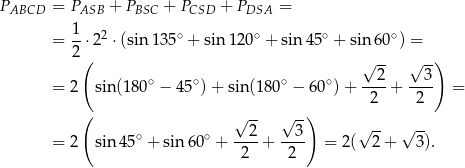
Odpowiedź: C

