Zadanie nr 7725975
Dany jest trójkąt 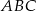 , w którym
, w którym 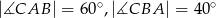 . Odcinki
. Odcinki 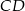 i
i 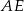 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 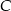 i
i 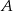 tego trójkąta. Zatem kąt
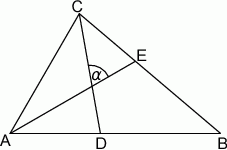
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
A) 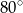 B)
B) 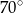 C)
C) 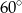 D)
D) 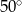
Rozwiązanie
Niech 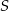 będzie punktem wspólnym dwusiecznych.
będzie punktem wspólnym dwusiecznych.
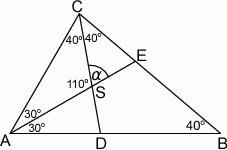
Liczymy
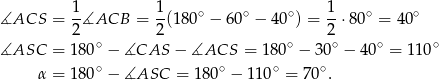
Odpowiedź: B

