Zadanie nr 8099989
Dany jest romb o boku długości 4 i polu równym 8. Kąt rozwarty tego rombu ma miarę
A) 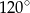 B)
B) 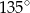 C)
C) 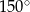 D)
D) 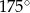
Rozwiązanie
Najpierw szkicowy rysunek.
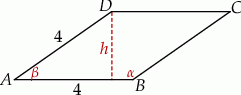
Sposób I
Korzystamy ze wzoru na pole równoległoboku z sinusem
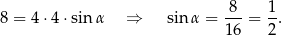
Ponieważ kąt  jest rozwarty, oznacza to, że
jest rozwarty, oznacza to, że
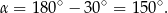
Sposób II
Z podanego pola możemy łatwo obliczyć wysokość 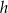 rombu
rombu
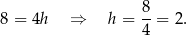
Jeżeli teraz 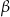 jest kątem ostrym rombu, to
jest kątem ostrym rombu, to
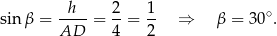
Zatem
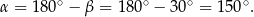
Odpowiedź: C

