/Szkoła średnia/Zadania testowe/Geometria/Planimetria

Zadanie nr 9533602

Dodaj do ulubionych
Dodaj do rozwiązanych

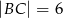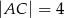Dane są długości boków |BC | = 6 i |AC | = 4 trójkąta prostokątnego 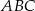ABC o kącie ostrym 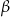β (zobacz rysunek).

PIC

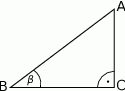
Wtedy
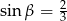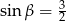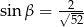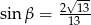
A) sin β = 23 B) sin β = 32 C) -2-- sin β = √52 D) 2√-13 sin β = 13

Rozwiązanie

Aby obliczyć sinus kąta 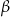β musimy najpierw wyliczyć długość przeciwprostokątnej (z twierdzenia Pitagorasa).

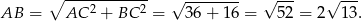
∘ ------------ √ -------- √ --- √ --- AB = AC 2 + BC 2 = 36+ 16 = 52 = 2 13.

Zatem sinus jest równy

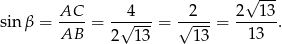
√ --- sin β = AC--= -√4---= √-2--= 2--13-. AB 2 13 13 13

 
Odpowiedź: D

Wersja PDF