/Szkoła średnia/Zadania testowe/Geometria/Planimetria

Zadanie nr 9860101

Dodaj do ulubionych
Dodaj do rozwiązanych

Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta styczna do okręgu o promieniu 3 w punkcie 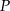P przechodzi przez środek okręgu o promieniu 4 (zobacz rysunek).

PIC

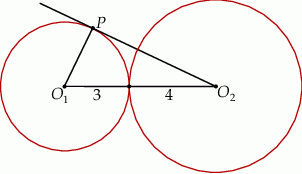
Pole trójkąta, którego wierzchołkami są środki okręgów i punkt styczności 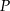P , jest równe
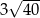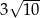A) 21 B) 3 √ 40- C) √ --- 3 1 0 D) 24

Rozwiązanie

Ponieważ styczna jest prostopadła do promienia 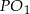PO 1 , to trójkąt 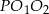PO 1O 2 jest prostokątny. Ponadto 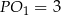P O 1 = 3 i

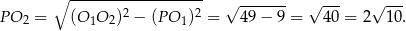
∘ ------------------- √ ------- √ --- √ --- PO 2 = (O1O 2)2 − (PO 1)2 = 49 − 9 = 40 = 2 10.

Pole trójkąta 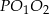P O1O 2 jest więc równe

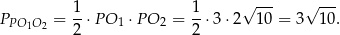
1 1 √ --- √ --- PPO1O2 = 2 ⋅ PO 1 ⋅P O 2 = 2-⋅3 ⋅2 10 = 3 10.

 
Odpowiedź: C

Wersja PDF