Zadanie nr 6513291
W trójkącie prostokątnym długości przyprostokątnych wynoszą 6 i 8. Stosunek długości odcinków, na które wysokość podzieliła przeciwprostokątną wynosi
A)  B)
B)  C)
C) 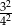 D)
D) 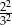
Rozwiązanie
Zaczynamy od rysunku
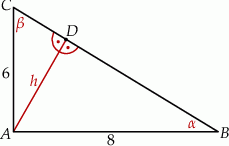
Sposób I
Trójkąty 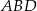 i
i 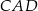 są prostokątne i każdy z nich ma kąt wspólny z trójkątem
są prostokątne i każdy z nich ma kąt wspólny z trójkątem 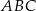 . Zatem każdy z nich jest podobny do trójkąta
. Zatem każdy z nich jest podobny do trójkąta 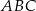 . Stąd
. Stąd
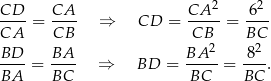
Stąd
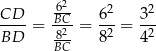
Sposób II
Przeciwprostokątna 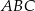 trójkąta ma długość
trójkąta ma długość
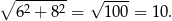
Obliczmy jeszcze długość wysokości trójkąta – porównujemy dwa wzory na jego pole.
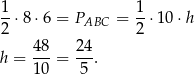
Stosujemy teraz twierdzenie Pitagorasa w trójkątach 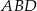 i
i 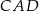 .
.
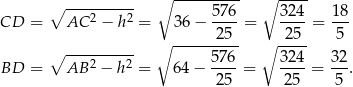
Stąd
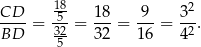
Odpowiedź: C

