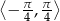/Szkoła średnia/Nierówności/Trygonometryczne

Zadanie nr 5973432

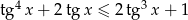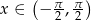Rozwiąż nierówność 4 3 tg x + 2 tg x ≤ 2 tg x + 1 , gdzie ( π- π) x ∈ − 2 ,2 .

Wersja PDF

Rozwiązanie

Podstawiamy 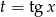t = tg x .

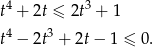
4 3 t + 2t ≤ 2t + 1 t4 − 2t3 + 2t− 1 ≤ 0.

Lewą stronę możemy rozłożyć na czynniki szukając pierwiastków wymiernych, ale prościej jest zauważyć, że łatwo możemy pogrupować składniki tak, aby wyłączyć 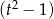2 (t − 1 ) .

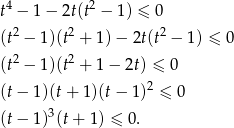
4 2 t − 1− 2t(t − 1) ≤ 0 (t2 − 1 )(t2 + 1) − 2t(t2 − 1) ≤ 0 2 2 (t − 1 )(t + 1 − 2t) ≤ 0 2 (t− 1)(t+ 1)(t − 1) ≤ 0 (t− 1)3(t+ 1) ≤ 0 .

Powyższa nierówność jest równoważna nierówności

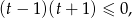
(t− 1 )(t+ 1) ≤ 0 ,

której rozwiązaniem jest przedział 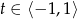t ∈ ⟨− 1,1⟩ . Mamy więc

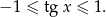
− 1 ≤ tgx ≤ 1.

Jeżeli naszkicujemy funkcję 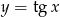y = tg x

PIC

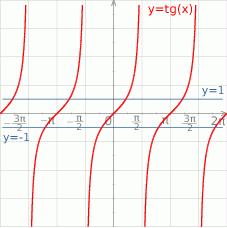
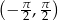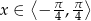to widać, że w przedziale ( ) − π2, π2 rozwiązaniem powyższej nierówności jest przedział ⟨ ⟩ x ∈ − π4, π4 .  
Odpowiedź: ⟨− π, π-⟩ 4 4

Wersja PDF