Zadanie nr 7223801
Rozwiąż nierówność 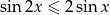 .
.
Rozwiązanie
Korzystamy ze wzoru
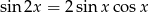
Mamy więc
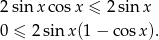
Ponieważ zawsze 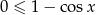 to nierówność ta jest równoważna nierówności
to nierówność ta jest równoważna nierówności
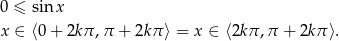
Odpowiedź: 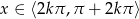 ,
, 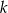 – całkowite.
– całkowite.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż nierówność 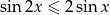 .
.
Korzystamy ze wzoru
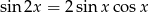
Mamy więc
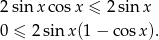
Ponieważ zawsze 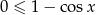 to nierówność ta jest równoważna nierówności
to nierówność ta jest równoważna nierówności
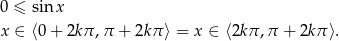
Odpowiedź: 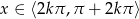 ,
, 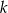 – całkowite.
– całkowite.
