/Szkoła średnia/Nierówności/Trygonometryczne

Zadanie nr 9739947

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 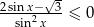2-sinx−√-3 sin2x ≤ 0 w przedziale ⟨0,2π ⟩ .

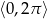Rozwiązanie

Oczywiście mianownik musi być niezerowy, czyli 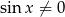sin x ⁄= 0 .

PIC

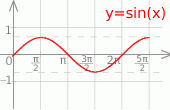
W podanym przedziale to oznacza, że

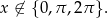
x ⁄∈ {0,π ,2π }.

Przy tym założeniu mianownik automatycznie jest dodatni, więc pozostaje do rozwiązania nierówność

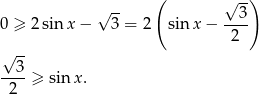
( √ -) √ -- 3 0 ≥ 2 sin x − 3 = 2 sinx − ---- 2 √ 3- ----≥ sin x. 2

Ponieważ 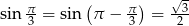π- ( π-) √-3 sin 3 = sin π − 3 = 2 , rozwiązaniem tej nierówności jest zbiór

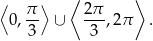
⟨ ⟩ ⟨ ⟩ 0, π ∪ 2π-,2π . 3 3

Uwzględniając warunek 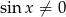sin x ⁄= 0 otrzymujemy

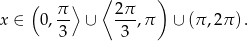
( ⟩ ⟨ ) x ∈ 0, π ∪ 2π-,π ∪ (π,2π ). 3 3

 
Odpowiedź: 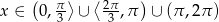( π⟩ ⟨2π- ) x ∈ 0 ,3 ∪ 3 ,π ∪ (π,2 π) .

Wersja PDF