Zadanie nr 1990845
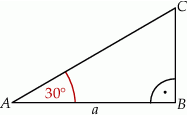
Obwód trójkąta 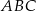 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy
A) 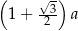 B)
B) 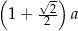 C)
C) 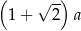 D)
D) 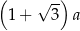
Rozwiązanie
Sposób I
Dany trójkąt to połówka trójkąta równobocznego, więc jeżeli oznaczymy 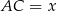 , to
, to
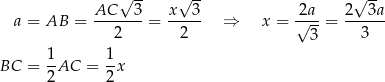
Obwód trójkąta 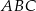 jest więc równy
jest więc równy
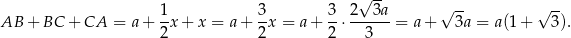
Sposób II
Korzystamy z funkcji trygonometrycznych.
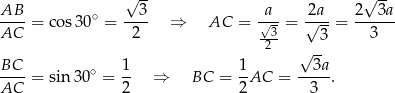
Obwód trójkąta 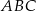 jest więc równy
jest więc równy
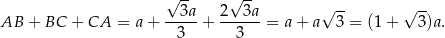
Odpowiedź: D

