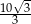Okręgi o środkach 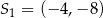 oraz
oraz 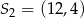 są styczne wewnętrznie. Promień pierwszego z tych okręgów jest 6 razy większy od promienia drugiego okręgu. Suma promieni tych okręgów jest równa
są styczne wewnętrznie. Promień pierwszego z tych okręgów jest 6 razy większy od promienia drugiego okręgu. Suma promieni tych okręgów jest równa
A) 28 B) 24 C) 20 D) 16
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna
Okrąg o środku 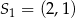 i promieniu
i promieniu  oraz okrąg o środku
oraz okrąg o środku 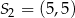 i promieniu 6 są styczne wewnętrznie. Wtedy
i promieniu 6 są styczne wewnętrznie. Wtedy
A) 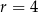 B)
B) 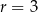 C)
C) 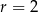 D)
D) 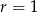
Punkt 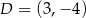 jest obrazem punktu
jest obrazem punktu 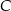 w symetrii względem punktu
w symetrii względem punktu 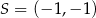 , a punkt
, a punkt 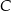 jest środkiem odcinka
jest środkiem odcinka 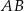 , gdzie
, gdzie 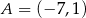 . Punkt
. Punkt 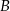 ma współrzędne
ma współrzędne
A) 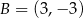 B)
B) 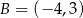 C)
C) 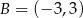 D)
D) 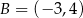
Punkt 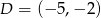 jest obrazem punktu
jest obrazem punktu 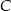 w symetrii względem punktu
w symetrii względem punktu 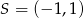 , a punkt
, a punkt 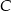 jest środkiem odcinka
jest środkiem odcinka 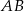 , gdzie
, gdzie 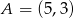 . Punkt
. Punkt 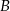 ma współrzędne
ma współrzędne
A) 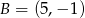 B)
B) 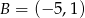 C)
C) 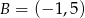 D)
D) 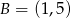
Punkt 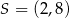 jest środkiem odcinka
jest środkiem odcinka 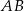 , gdzie
, gdzie 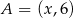 i
i 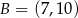 dla
dla  równego
równego
A) 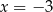 B)
B) 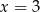 C)
C) 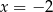 D)
D) 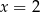
Dane są punkty 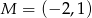 i
i 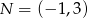 . Punkt
. Punkt 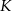 jest środkiem odcinka
jest środkiem odcinka 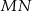 . Obrazem punktu
. Obrazem punktu 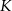 w symetrii względem początku układu współrzędnych jest punkt
w symetrii względem początku układu współrzędnych jest punkt
A) 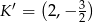 B)
B) 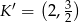 C)
C) 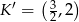 D)
D) 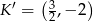
Dane są punkty 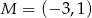 i
i 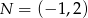 . Punkt
. Punkt 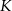 jest środkiem odcinka
jest środkiem odcinka 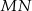 . Obrazem punktu
. Obrazem punktu 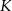 w symetrii względem początku układu współrzędnych jest punkt
w symetrii względem początku układu współrzędnych jest punkt
A) 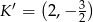 B)
B) 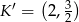 C)
C) 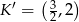 D)
D) 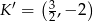
Proste o równaniach: 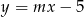 i
i 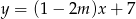 są równoległe, gdy
są równoległe, gdy
A) 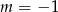 B)
B) 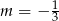 C)
C) 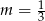 D)
D) 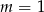
Proste o równaniach 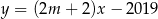 i
i 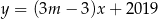 są równoległe, gdy
są równoległe, gdy
A) 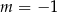 B)
B) 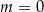 C)
C) 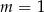 D)
D) 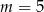
Prosta 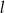 o równaniu
o równaniu 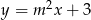 jest równoległa do prostej
jest równoległa do prostej 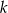 o równaniu
o równaniu 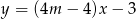 . Zatem
. Zatem
A) 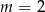 B)
B) 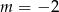 C)
C) 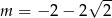 D)
D) 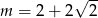
Proste o równaniach 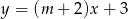 i
i 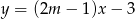 są równoległe, gdy
są równoległe, gdy
A) 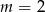 B)
B) 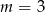 C)
C) 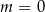 D)
D) 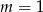
Prosta 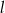 o równaniu
o równaniu 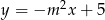 jest równoległa do prostej
jest równoległa do prostej 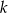 o równaniu
o równaniu 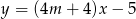 . Zatem
. Zatem
A) 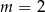 B)
B) 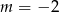 C)
C) 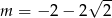 D)
D) 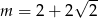
Proste o równaniach 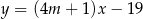 i
i 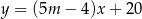 są równoległe, gdy
są równoległe, gdy
A) 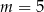 B)
B) 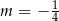 C)
C) 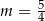 D)
D) 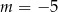
Proste o równaniach: 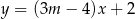 i
i 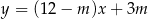 są równoległe, gdy
są równoległe, gdy
A) 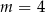 B)
B) 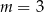 C)
C) 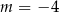 D)
D) 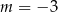
Proste o równaniach 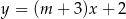 i
i 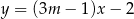 są równoległe, gdy
są równoległe, gdy
A) 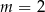 B)
B) 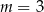 C)
C) 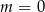 D)
D) 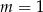
Punkty 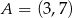 i
i 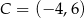 są końcami przekątnej kwadratu
są końcami przekątnej kwadratu 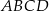 . Promień okręgu opisanego na tym kwadracie jest równy
. Promień okręgu opisanego na tym kwadracie jest równy
A) 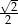 B)
B)  C)
C) 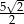 D) 5
D) 5
Punkty 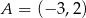 i
i 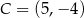 są końcami przekątnej kwadratu
są końcami przekątnej kwadratu 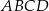 . Promień okręgu opisanego na tym kwadracie jest równy
. Promień okręgu opisanego na tym kwadracie jest równy
A) 100 B) 50 C) 10 D) 5
Dwa przeciwległe wierzchołki prostokąta mają współrzędne 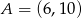 i
i 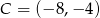 . Środek okręgu opisanego na tym prostokącie leży na prostej
. Środek okręgu opisanego na tym prostokącie leży na prostej
A) 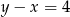 B)
B) 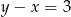 C)
C) 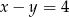 D)
D) 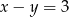
Dany jest trójkąt o wierzchołkach 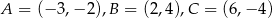 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 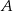 jest równa
jest równa
A) 4 B) 6 C) 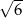 D)
D) 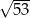
Dany jest trójkąt o wierzchołkach 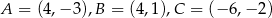 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 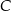 jest równa
jest równa
A) 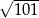 B)
B) 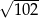 C)
C) 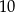 D)
D) 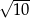
Dany jest trójkąt o wierzchołkach 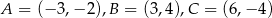 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 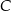 jest równa
jest równa
A) 11 B) 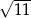 C)
C) 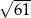 D)
D) 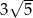
Dany jest trójkąt o wierzchołkach 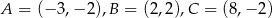 . Długość środkowej poprowadzonej z wierzchołka
. Długość środkowej poprowadzonej z wierzchołka 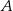 jest równa
jest równa
A) 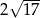 B)
B) 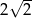 C)
C) 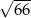 D)
D) 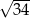
Prosta o równaniu 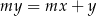 nie przecina prostej
nie przecina prostej 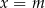 . Zatem
. Zatem
A) 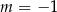 B)
B) 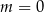 C)
C) 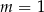 D)
D) 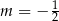
Punkty 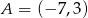 i
i 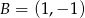 są wierzchołkami pięciokąta foremnego
są wierzchołkami pięciokąta foremnego 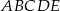 . Obwód tego pięciokąta jest równy
. Obwód tego pięciokąta jest równy
A) 50 B) 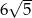 C) 60 D)
C) 60 D) 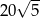
Punkty 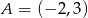 i
i 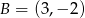 są wierzchołkami sześciokąta foremnego
są wierzchołkami sześciokąta foremnego 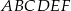 . Obwód tego sześciokąta jest równy
. Obwód tego sześciokąta jest równy
A) 50 B) 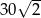 C) 300 D)
C) 300 D) 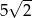
Dane są punkty 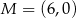 ,
, 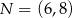 oraz
oraz 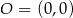 . Tangens kąta ostrego
. Tangens kąta ostrego 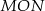 jest równy
jest równy
A) 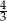 B)
B) 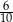 C)
C)  D)
D) 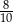
Dane są punkty 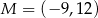 ,
, 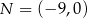 oraz
oraz 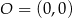 . Tangens kąta ostrego
. Tangens kąta ostrego 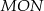 jest równy
jest równy
A) 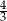 B)
B) 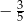 C)
C)  D)
D) 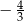
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 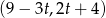 , gdzie
, gdzie 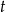 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 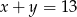 B)
B) 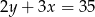 C)
C) 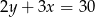 D)
D) 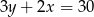
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 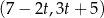 , gdzie
, gdzie 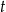 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 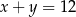 B)
B) 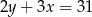 C)
C) 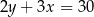 D)
D) 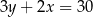
Proste prostopadłe 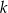 i
i 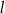 o równaniach
o równaniach 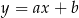 oraz
oraz 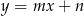 przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
A) obie liczby 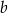 i
i  mogą być ujemne B) obie liczby
mogą być ujemne B) obie liczby 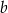 i
i  mogą być dodatnie
mogą być dodatnie
C) obie liczby 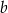 i
i  muszą być ujemne D) obie liczby
muszą być ujemne D) obie liczby 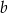 i
i  muszą być dodatnie
muszą być dodatnie
Liczba punktów wspólnych okręgu 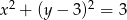 i prostej
i prostej 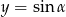 , gdzie
, gdzie  jest kątem ostrym jest równa
jest kątem ostrym jest równa
A) 0 B) 1 C) 2 D) 3
Liczba punktów wspólnych okręgu 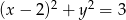 i prostej
i prostej 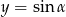 , gdzie
, gdzie  jest kątem ostrym jest równa
jest kątem ostrym jest równa
A) 0 B) 1 C) 2 D) 3
Liczba punktów wspólnych okręgu 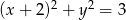 i prostej
i prostej 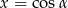 , gdzie
, gdzie  jest kątem ostrym jest równa
jest kątem ostrym jest równa
A) 3 B) 2 C) 1 D) 0
Prostymi równoległymi są wykresy funkcji liniowych:
A) 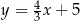 i
i 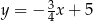 B)
B) 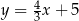 i
i 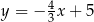
C) 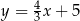 i
i 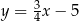 D)
D) 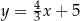 i
i 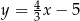
Ramię końcowe kąta 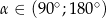 zawiera się w prostej
zawiera się w prostej 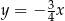 . Zatem
. Zatem
A) 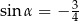 B)
B) 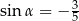 C)
C) 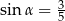 D)
D) 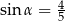
Punkty 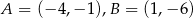 i
i 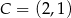 są trzema kolejnymi wierzchołkami rombu
są trzema kolejnymi wierzchołkami rombu 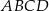 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 40 B) 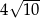 C) 80 D) 20
C) 80 D) 20
Punkty 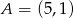 oraz
oraz 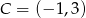 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 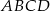 . Bok tego kwadratu ma długość:
. Bok tego kwadratu ma długość:
A) 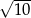 B)
B) 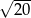 C)
C) 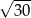 D)
D) 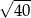
Punkty 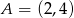 oraz
oraz 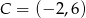 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 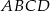 . Bok tego kwadratu ma długość:
. Bok tego kwadratu ma długość:
A) 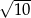 B)
B) 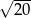 C)
C) 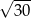 D)
D) 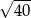
Punkty 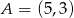 oraz
oraz 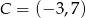 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 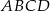 . Bok tego kwadratu ma długość:
. Bok tego kwadratu ma długość:
A) 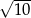 B)
B) 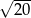 C)
C) 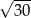 D)
D) 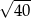
Punkt 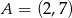 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 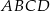 , a punkt
, a punkt 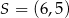 jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
A) 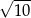 B)
B) 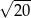 C)
C) 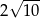 D)
D) 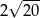
Punkt 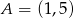 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 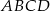 , a punkt
, a punkt 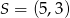 jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
A) 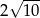 B)
B) 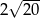 C)
C) 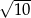 D)
D) 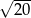
Dane są punkty 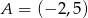 oraz
oraz 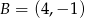 . Promień okręgu opisanego na trójkącie równobocznym
. Promień okręgu opisanego na trójkącie równobocznym 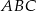 jest równy
jest równy
A) 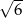 B)
B) 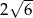 C)
C) 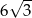 D)
D) 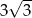
Punkty 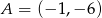 i
i 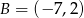 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 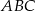 . Promień koła opisanego na tym trójkącie jest równy
. Promień koła opisanego na tym trójkącie jest równy
A) 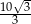 B)
B) 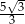 C)
C) 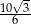 D)
D) 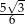
Punkty 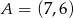 i
i 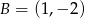 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 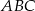 . Promień koła opisanego na tym trójkącie jest równy
. Promień koła opisanego na tym trójkącie jest równy
A) 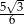 B)
B) 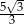 C)
C) 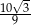 D)
D)