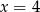Suma dziesięciu początkowych wyrazów ciągu arytmetycznego 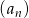 jest równa 35. Pierwszy wyraz
jest równa 35. Pierwszy wyraz 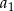 tego ciągu jest równy 3. Wtedy
tego ciągu jest równy 3. Wtedy
A) 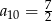 B)
B) 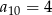 C)
C) 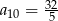 D)
D) 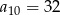
/Szkoła średnia/Zadania testowe/Ciągi
Suma dwunastu początkowych wyrazów ciągu arytmetycznego 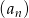 jest równa 42. Pierwszy wyraz
jest równa 42. Pierwszy wyraz 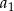 tego ciągu jest równy 4. Wtedy
tego ciągu jest równy 4. Wtedy
A) 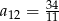 B)
B) 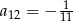 C)
C) 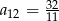 D)
D) 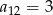
Wyraz ogólny ciągu 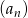 jest równy
jest równy 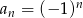 . Zatem
. Zatem 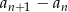 równa się
równa się
A) 0 B) 1 C) 2 lub -2 D) -2 lub 0
Wyraz ogólny ciągu 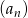 jest równy
jest równy 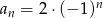 . Zatem
. Zatem 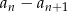 równa się
równa się
A) 0 B) 1 C) 2 lub -2 D) -4 lub 4
Wyraz ogólny ciągu 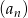 jest równy
jest równy 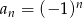 . Zatem
. Zatem 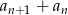 równa się
równa się
A) 0 B) 1 C) 2 lub -2 D) -1 lub 1
Czterowyrazowy ciąg 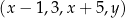 jest arytmetyczny. Liczba
jest arytmetyczny. Liczba 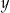 jest równa
jest równa
A) 6 B) 7 C) 13 D) 9
W ciągu arytmetycznym 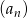 dane są:
dane są: 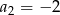 i
i 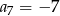 . Wtedy
. Wtedy
A) 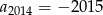 B)
B) 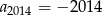 C)
C) 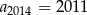 D)
D) 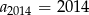
Drugi wyraz ciągu arytmetycznego jest równy 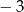 , a dziesiąty wyraz jest równy 21. Szósty wyraz tego ciągu ma wartość
, a dziesiąty wyraz jest równy 21. Szósty wyraz tego ciągu ma wartość
A) 8 B) 9 C) 6 D) 12
Na tablicy wypisano kolejne wyrazy pewnego ciągu arytmetycznego
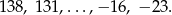
Ile liczb napisano na tablicy?
A) 21 B) 22 C) 23 D) 24
Na tablicy wypisano kolejne wyrazy pewnego ciągu arytmetycznego
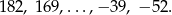
Ile liczb napisano na tablicy?
A) 17 B) 18 C) 19 D) 20
W ciągu geometrycznym 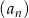 dane są:
dane są: 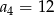 i
i 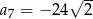 . Iloraz ciągu
. Iloraz ciągu 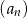 jest równy
jest równy
A) 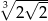 B)
B) 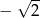 C)
C) 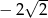 D)
D) 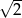
Suma 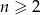 początkowych wyrazów ciągu
początkowych wyrazów ciągu 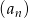 opisana jest wzorem
opisana jest wzorem 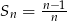 . Wyraz
. Wyraz 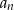 dla
dla 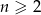 tego ciągu jest równy
tego ciągu jest równy
A) 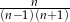 B)
B)  C)
C) 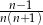 D)
D) 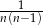
Suma 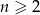 początkowych wyrazów ciągu
początkowych wyrazów ciągu 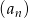 opisana jest wzorem
opisana jest wzorem 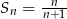 . Wyraz
. Wyraz 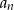 dla
dla 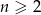 tego ciągu jest równy
tego ciągu jest równy
A) 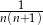 B)
B) 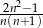 C)
C) 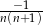 D)
D) 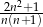
Suma 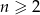 początkowych wyrazów ciągu
początkowych wyrazów ciągu 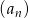 opisana jest wzorem
opisana jest wzorem 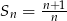 . Wyraz
. Wyraz 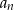 dla
dla 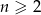 tego ciągu jest równy
tego ciągu jest równy
A) 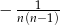 B)
B)  C)
C) 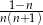 D)
D) 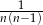
Liczby 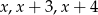 tworzą ciąg geometryczny. Wynika stąd, że
tworzą ciąg geometryczny. Wynika stąd, że
A) 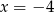 B)
B) 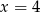 C)
C) 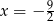 D)
D) 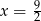
Ciąg 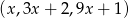 jest geometryczny. Pierwszy wyraz tego ciągu jest równy
jest geometryczny. Pierwszy wyraz tego ciągu jest równy
A) 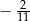 B)
B) 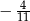 C)
C) 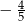 D)
D) 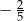
Liczby 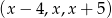 tworzą ciąg geometryczny dla
tworzą ciąg geometryczny dla
A) 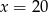 B)
B) 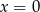 C)
C) 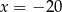 D)
D) 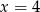
Dla pewnej liczby  ciąg
ciąg 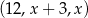 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 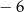 B) 9 C) 6 D) 3
B) 9 C) 6 D) 3
Liczby 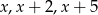 tworzą ciąg geometryczny. Wynika stąd, że
tworzą ciąg geometryczny. Wynika stąd, że
A) 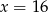 B)
B) 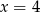 C)
C) 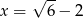 D)
D) 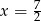
Dla pewnej liczby  ciąg
ciąg 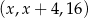 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 8 B) 4 C) 2 D) 0
Ciąg 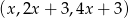 jest geometryczny. Pierwszy wyraz tego ciągu jest równy
jest geometryczny. Pierwszy wyraz tego ciągu jest równy
A) 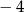 B) 1 C) 0 D)
B) 1 C) 0 D) 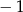
Ciąg 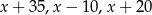 jest geometryczny. Stąd wynika, że
jest geometryczny. Stąd wynika, że
A) 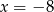 B)
B) 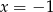 C)
C) 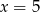 D)
D) 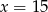
Liczby 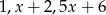 są kolejnymi wyrazami ciągu geometrycznego. Zatem liczba
są kolejnymi wyrazami ciągu geometrycznego. Zatem liczba  spełnia warunek
spełnia warunek
A) 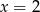 B)
B) 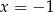 C)
C) 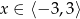 D)
D) 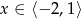
Granica 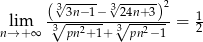 . Wynika stąd, że
. Wynika stąd, że
A) 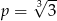 B)
B) 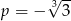 C)
C) 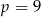 D)
D) 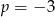
Ciąg 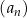 jest określony wzorem
jest określony wzorem
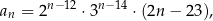
dla każdej liczby naturalnej 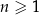 . Który wyraz ciągu
. Który wyraz ciągu 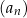 jest równy 466 560?
jest równy 466 560?
A) 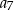 B)
B) 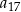 C)
C) 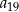 D)
D) 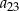
Granica
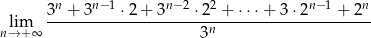
jest równa
A) 2 B) 3 C) 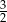 D) 0
D) 0
W dziewięciowyrazowym ciągu geometrycznym o wyrazach dodatnich pierwszy wyraz jest równy 3, a ostatni wyraz jest równy 12. Piąty wyraz tego ciągu jest równy
A) 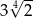 B) 6 C)
B) 6 C) 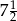 D)
D) 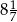
W jedenastowyrazowym ciągu geometrycznym o wyrazach dodatnich pierwszy wyraz jest równy 4, a ostatni wyraz jest równy 36. Szósty wyraz tego ciągu jest równy
A) 12 B) 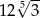 C)
C) 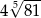 D) 20
D) 20
Dany jest nieskończony rosnący ciąg geometryczny 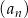 o wyrazach dodatnich. Iloraz
o wyrazach dodatnich. Iloraz 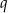 tego ciągu jest jednym z pierwiastków równania kwadratowego
tego ciągu jest jednym z pierwiastków równania kwadratowego 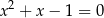 . Zatem wartość wyrażenia
. Zatem wartość wyrażenia
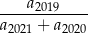
jest równa
A) 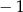 B)
B) 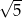 C)
C) 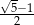 D) 1
D) 1
Liczby 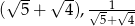 są początkowymi wyrazami ciągu arytmetycznego. Trzeci wyraz tego ciągu jest równy
są początkowymi wyrazami ciągu arytmetycznego. Trzeci wyraz tego ciągu jest równy
A) 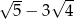 B)
B) 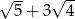 C)
C) 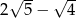 D)
D) 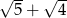
Liczby 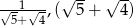 są początkowymi wyrazami ciągu arytmetycznego. Trzeci wyraz tego ciągu jest równy
są początkowymi wyrazami ciągu arytmetycznego. Trzeci wyraz tego ciągu jest równy
A) 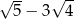 B)
B) 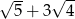 C)
C) 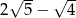 D)
D) 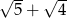
Liczby 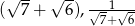 są początkowymi wyrazami ciągu arytmetycznego. Trzeci wyraz tego ciągu jest równy
są początkowymi wyrazami ciągu arytmetycznego. Trzeci wyraz tego ciągu jest równy
A) 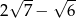 B)
B) 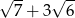 C)
C) 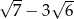 D)
D) 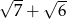
Dany jest nieskończony rosnący ciąg arytmetyczny 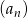 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 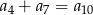 B)
B) 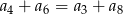 C)
C) 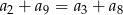 D)
D) 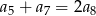
Dany jest nieskończony rosnący ciąg arytmetyczny 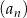 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 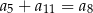 B)
B) 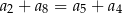 C)
C) 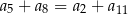 D)
D) 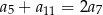
Dany jest nieskończony rosnący ciąg arytmetyczny 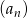 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 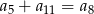 B)
B) 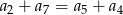 C)
C) 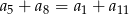 D)
D) 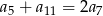
Liczby 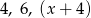 są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas liczba
są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas liczba  jest równa:
jest równa:
A) 9 B) 10 C) 13 D) 5
Trójwyrazowy ciąg 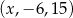 jest ciągiem geometrycznym. Wtedy
jest ciągiem geometrycznym. Wtedy
A) 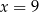 B)
B) 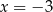 C)
C) 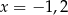 D)
D) 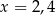
Liczby: 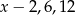 , w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba
, w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba  jest równa
jest równa
A) 0 B) 2 C) 3 D) 5
Ciąg 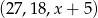 jest geometryczny. Wtedy
jest geometryczny. Wtedy
A) 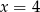 B)
B) 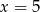 C)
C) 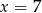 D)
D) 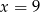
Liczby 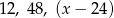 są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas trzeci wyraz tego ciągu jest równy:
są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas trzeci wyraz tego ciągu jest równy:
A) 192 B) 216 C) 60 D) 24
Liczby 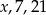 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba  jest równa
jest równa
A) 1 B)  C)
C) 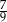 D)
D) 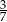
Liczby 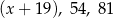 są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas pierwszy wyraz tego ciągu jest równy:
są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas pierwszy wyraz tego ciągu jest równy:
A) 62 B) 36 C) 35 D) 17
Ciąg 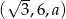 jest geometryczny. Wówczas
jest geometryczny. Wówczas
A) 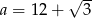 B)
B) 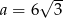 C)
C) 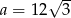 D)
D) 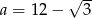
Trzywyrazowy ciąg 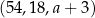 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 3 B) 6 C) 4 D) 2
Dany jest ciąg liczbowy 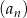 , w którym
, w którym 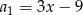 ,
, 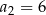 ,
, 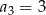 . Dla jakiej wartości liczbowej
. Dla jakiej wartości liczbowej  dany ciąg jest ciągiem geometrycznym?
dany ciąg jest ciągiem geometrycznym?
A) 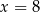 B)
B) 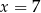 C)
C) 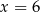 D)
D) 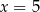
Trzywyrazowy ciąg 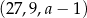 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 3 B) 0 C) 4 D) 2
Liczby 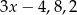 w podanej kolejności są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wtedy
w podanej kolejności są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wtedy
A) 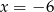 B)
B) 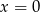 C)
C) 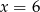 D)
D) 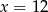
Trzywyrazowy ciąg 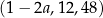 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 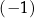 B) 3 C) 4 D) 12,5
B) 3 C) 4 D) 12,5
Ciąg 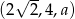 jest geometryczny. Wówczas
jest geometryczny. Wówczas
A) 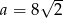 B)
B) 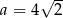 C)
C) 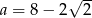 D)
D) 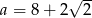
Dany jest trzywyrazowy ciąg geometryczny 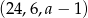 . Stąd wynika, że
. Stąd wynika, że
A) 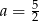 B)
B) 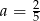 C)
C) 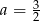 D)
D) 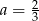
Trzywyrazowy ciąg 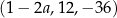 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 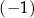 B) 5 C) 4 D) 2,5
B) 5 C) 4 D) 2,5
Ciąg 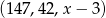 jest geometryczny. Wtedy
jest geometryczny. Wtedy
A) 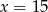 B)
B) 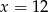 C)
C) 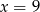 D)
D) 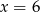
Liczby 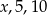 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba  jest równa
jest równa
A) 2,5 B) 5 C) 10 D) 0
Liczby 9,-3 i 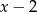 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba  jest równa
jest równa
A) 1 B) -1,5 C) 5 D) 3
Liczby -8,4 i 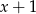 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba  jest równa
jest równa
A) -3 B) -1,5 C) 1 D) 15
Ciąg 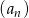 jest rosnącym ciągiem geometrycznym o ilorazie
jest rosnącym ciągiem geometrycznym o ilorazie 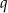 , gdzie
, gdzie 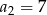 i
i 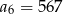 . Zatem:
. Zatem:
A) 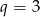 lub
lub 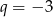 B)
B) 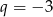 C)
C) 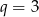 D)
D) 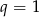
Trzeci wyraz pewnego ciągu geometrycznego jest równy 6, a szósty wyraz ma wartość 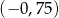 . Iloraz tego ciągu jest równy:
. Iloraz tego ciągu jest równy:
A) 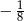 B)
B) 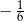 C)
C) 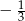 D)
D) 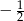
Ciąg 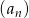 spełnia warunek
spełnia warunek 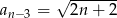 dla
dla 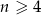 . Wówczas
. Wówczas
A) 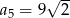 B)
B) 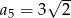 C)
C) 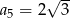 D)
D) 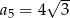
Suma pierwszego i szóstego wyrazu pewnego ciągu arytmetycznego jest równa 13 . Wynika stąd, że suma trzeciego i czwartego wyrazu tego ciągu jest równa
A) 13 B) 12 C) 7 D) 6
Suma pierwszego i siódmego wyrazu pewnego ciągu arytmetycznego jest równa 17 . Wynika stąd, że suma trzeciego i piątego wyrazu tego ciągu jest równa
A) 7 B) 16 C) 17 D) 6
Dany jest ciąg geometryczny
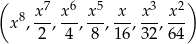
o wyrazach dodatnich. Wtedy
A) 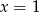 B)
B) 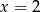 C)
C) 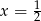 D)
D)