/Szkoła średnia/Zadania testowe/Ciągi

Zadanie nr 3495550

Dodaj do ulubionych
Dodaj do rozwiązanych

Drugi wyraz ciągu arytmetycznego jest równy 10, a trzeci wyraz jest równy 6. Wzór na ogólny wyraz tego ciągu to
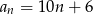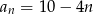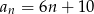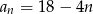
A) an = 1 0n + 6 B) an = 1 0− 4n C) an = 6n + 10 D) an = 18 − 4n

Rozwiązanie

Przypomnijmy, że wzór na ogólny wyraz ciągu, to

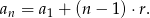
an = a1 + (n − 1) ⋅r.

Wyznaczamy różnicę r

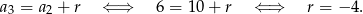
a3 = a2 + r ⇐ ⇒ 6 = 10+ r ⇐ ⇒ r = − 4.

Wyznaczamy pierwszy wyraz ciągu

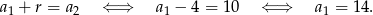
a1 + r = a2 ⇐ ⇒ a1 − 4 = 10 ⇐ ⇒ a 1 = 14.

Teraz już łatwo zapisać wzór na ogólny wyraz tego ciągu.

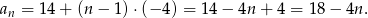
an = 14 + (n − 1 )⋅(− 4) = 14 − 4n + 4 = 18 − 4n .

 
Odpowiedź: D

Wersja PDF