/Szkoła średnia/Zadania testowe/Ciągi

Zadanie nr 7236940

Dodaj do ulubionych
Dodaj do rozwiązanych

Cztery liczby dodatnie 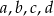a,b,c,d w podanej kolejności, tworzą ciąg geometryczny. Zatem liczby 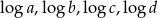lo ga,log b,logc,log d (w podanej kolejności) tworzą
A) ciąg geometryczny o ilorazie 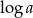log a
B) ciąg geometryczny o ilorazie 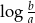b lo ga
C) ciąg arytmetyczny o różnicy 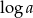log a
D) ciąg arytmetyczny o różnicy 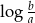lo g ba

Rozwiązanie

Oznaczmy przez 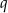q iloraz ciągu 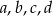a,b,c,d . Wówczas

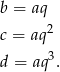
b = aq c = aq2 3 d = aq .

Zatem

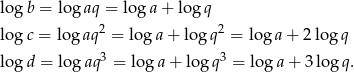
log b = lo gaq = lo ga + log q log c = lo gaq2 = lo ga + log q2 = loga + 2 logq log d = logaq 3 = lo ga + log q3 = log a+ 3log q.

Widać, że liczby 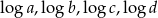log a,logb ,log c,log d tworzą ciąg arytmetyczny o różnicy równej 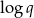log q . Zauważmy jeszcze, że

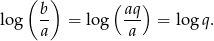
( ) b- (aq-) log a = log a = log q.

 
Odpowiedź: D

Wersja PDF