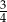Proste o równaniach: 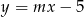 i
i 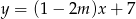 są równoległe, gdy
są równoległe, gdy
A) 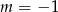 B)
B) 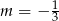 C)
C) 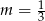 D)
D) 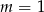
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Równanie prostej
Proste o równaniach 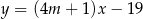 i
i 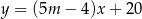 są równoległe, gdy
są równoległe, gdy
A) 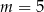 B)
B) 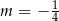 C)
C) 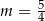 D)
D) 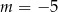
Prosta 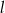 o równaniu
o równaniu 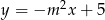 jest równoległa do prostej
jest równoległa do prostej 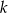 o równaniu
o równaniu 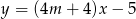 . Zatem
. Zatem
A) 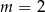 B)
B) 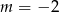 C)
C) 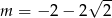 D)
D) 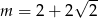
Proste o równaniach 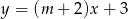 i
i 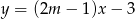 są równoległe, gdy
są równoległe, gdy
A) 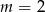 B)
B) 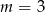 C)
C) 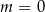 D)
D) 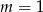
Prosta 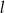 o równaniu
o równaniu 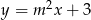 jest równoległa do prostej
jest równoległa do prostej 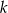 o równaniu
o równaniu 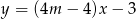 . Zatem
. Zatem
A) 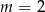 B)
B) 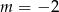 C)
C) 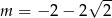 D)
D) 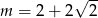
Proste o równaniach 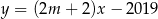 i
i 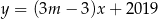 są równoległe, gdy
są równoległe, gdy
A) 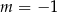 B)
B) 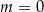 C)
C) 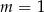 D)
D) 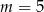
Proste o równaniach 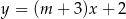 i
i 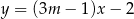 są równoległe, gdy
są równoległe, gdy
A) 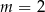 B)
B) 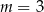 C)
C) 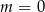 D)
D) 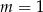
Proste o równaniach: 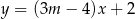 i
i 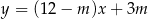 są równoległe, gdy
są równoległe, gdy
A) 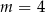 B)
B) 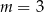 C)
C) 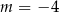 D)
D) 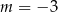
Prosta o równaniu 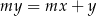 nie przecina prostej
nie przecina prostej 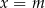 . Zatem
. Zatem
A) 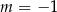 B)
B) 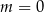 C)
C) 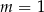 D)
D) 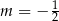
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 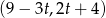 , gdzie
, gdzie 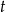 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 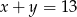 B)
B) 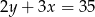 C)
C) 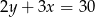 D)
D) 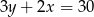
Na której z podanych prostych leżą wszystkie punkty o współrzędnych 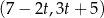 , gdzie
, gdzie 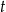 jest dowolną liczbą rzeczywistą?
jest dowolną liczbą rzeczywistą?
A) 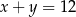 B)
B) 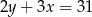 C)
C) 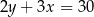 D)
D) 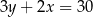
Proste prostopadłe 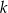 i
i 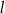 o równaniach
o równaniach 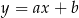 oraz
oraz 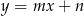 przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
przecinają się w punkcie o drugiej współrzędnej ujemnej. Zatem
A) obie liczby 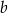 i
i  mogą być ujemne B) obie liczby
mogą być ujemne B) obie liczby 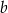 i
i  mogą być dodatnie
mogą być dodatnie
C) obie liczby 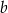 i
i  muszą być ujemne D) obie liczby
muszą być ujemne D) obie liczby 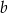 i
i  muszą być dodatnie
muszą być dodatnie
Prostymi równoległymi są wykresy funkcji liniowych:
A) 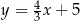 i
i 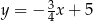 B)
B) 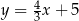 i
i 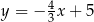
C) 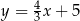 i
i 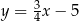 D)
D) 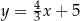 i
i 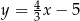
Ramię końcowe kąta 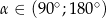 zawiera się w prostej
zawiera się w prostej 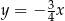 . Zatem
. Zatem
A) 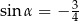 B)
B) 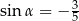 C)
C) 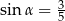 D)
D) 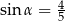
Prosta o równaniu 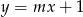 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 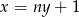 . Stąd wynika, że
. Stąd wynika, że
A) 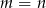 B)
B) 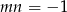 C)
C) 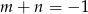 D)
D) 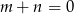
Prosta o równaniu 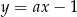 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 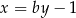 . Stąd wynika, że
. Stąd wynika, że
A) 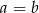 B)
B) 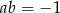 C)
C) 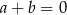 D)
D) 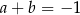
Dane są dwie proste równoległe 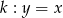 oraz
oraz 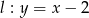 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 2 B) 1,5 C) 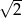 D) 1
D) 1
Odległość między prostymi 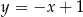 i
i 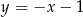 jest równa
jest równa
A) 2 B) 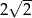 C) 1 D)
C) 1 D) 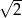
Dane są dwie proste równoległe 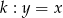 oraz
oraz 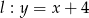 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 4 B) 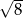 C)
C) 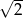 D) 3
D) 3
Dane są dwie proste równoległe 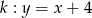 oraz
oraz 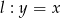 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 2 B) 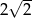 C)
C) 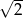 D) 4
D) 4
Dla jakiej wartości parametru 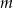 punkt przecięcia prostych
punkt przecięcia prostych 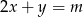 i
i 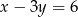 należy do osi
należy do osi 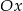 ?
?
A) dla 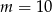 B) dla
B) dla 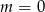 C) dla
C) dla 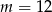 D) dla
D) dla 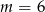
Proste o równaniach 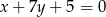 i
i 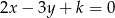 przecinają się na osi
przecinają się na osi 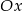 . Zatem parametr
. Zatem parametr 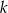 jest równy
jest równy
A) 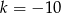 B)
B) 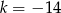 C)
C) 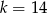 D)
D) 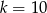
Odcinek o końcach 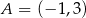 i
i 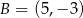 jest równoległy do prostej o równaniu
jest równoległy do prostej o równaniu
A) 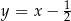 B)
B) 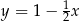 C)
C) 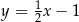 D)
D) 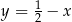
Punkty 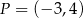 i
i 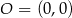 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem nachylenia tej prostej do osi
jest kątem nachylenia tej prostej do osi 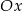 (zobacz rysunek).
(zobacz rysunek).
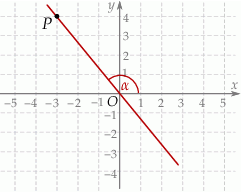
Wtedy tangens kąta  jest równy
jest równy
A) 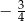 B)
B) 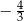 C)
C) 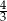 D)
D) 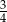
Punkty 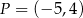 i
i 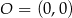 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem nachylenia tej prostej do osi
jest kątem nachylenia tej prostej do osi 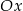 (zobacz rysunek).
(zobacz rysunek).
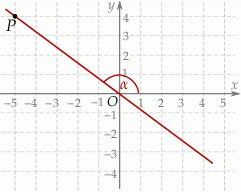
Wtedy tangens kąta  jest równy
jest równy
A)  B)
B)  C)
C) 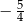 D)
D) 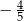
Punkt 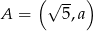 należy do prostej o równaniu
należy do prostej o równaniu 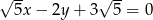 . Wynika stąd, że
. Wynika stąd, że
A) 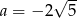 B)
B) 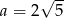 C)
C) 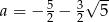 D)
D) 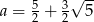
Punkt 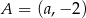 leży na prostej określonej równaniem
leży na prostej określonej równaniem 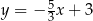 . Stąd wynika, że
. Stąd wynika, że
A) 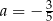 B)
B) 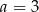 C)
C) 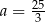 D)
D) 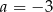
Punkt 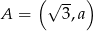 należy do prostej o równaniu
należy do prostej o równaniu 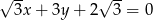 . Wynika stąd, że
. Wynika stąd, że
A) 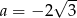 B)
B) 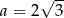 C)
C) 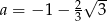 D)
D) 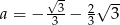
Punkt 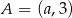 leży na prostej określonej równaniem
leży na prostej określonej równaniem 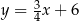 . Stąd wynika, że
. Stąd wynika, że
A) 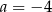 B)
B) 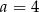 C)
C) 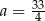 D)
D) 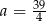
Punkt 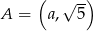 należy do prostej o równaniu
należy do prostej o równaniu 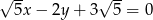 . Wynika stąd, że
. Wynika stąd, że
A) 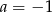 B)
B) 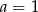 C)
C) 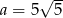 D)
D) 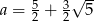
Równania 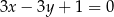 i
i 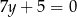 opisują proste w układzie współrzędnych, które
opisują proste w układzie współrzędnych, które
A) są prostopadłe B) są równoległe
C) przecinają się pod kątem 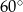 D) przecinają się pod kątem
D) przecinają się pod kątem 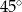
Równania 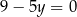 i
i 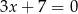 opisują proste w układzie współrzędnych, które
opisują proste w układzie współrzędnych, które
A) są prostopadłe B) są równoległe
C) przecinają się pod kątem 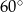 D) przecinają się pod kątem
D) przecinają się pod kątem 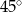
Prosta 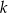 przechodzi przez punkt
przechodzi przez punkt 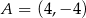 i jest prostopadła do osi
i jest prostopadła do osi 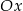 . Prosta
. Prosta 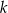 ma równanie
ma równanie
A) 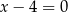 B)
B) 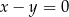 C)
C) 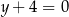 D)
D) 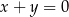
Prosta 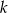 przechodzi przez punkt
przechodzi przez punkt 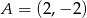 i jest prostopadła do osi
i jest prostopadła do osi 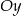 . Prosta
. Prosta 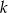 ma równanie
ma równanie
A) 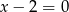 B)
B) 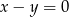 C)
C) 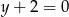 D)
D) 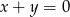
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 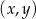 , dane są proste
, dane są proste 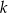 oraz
oraz 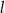 o równaniach
o równaniach
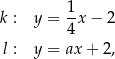
gdzie  jest pewną liczbą rzeczywistą. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest pewną liczbą rzeczywistą. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 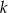 i i 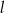 mogą mięc nieskończenie wiele punktów wspólnych. mogą mięc nieskończenie wiele punktów wspólnych. | P | F |
Punkt wspólny prostych 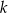 i i 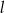 może leżeć w I ćwiartce układu współrzędnych może leżeć w I ćwiartce układu współrzędnych | P | F |
Które z danych równań opisuje prostą równoległą do osi 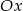 ?
?
A) 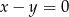 B)
B) 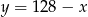 C)
C) 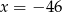 D)
D) 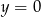
Które z danych równań opisuje prostą prostopadłą do osi 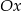 ?
?
A) 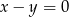 B)
B) 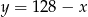 C)
C) 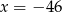 D)
D) 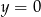
Na rysunku przedstawiono fragment prostej o równaniu 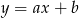 .
.
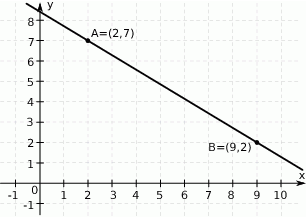
Punkt 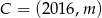 leży na tej prostej. Zatem
leży na tej prostej. Zatem
A) 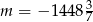 B)
B) 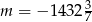 C)
C) 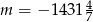 D)
D) 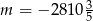
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 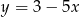 jest równy
jest równy
A) 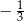 B) 3 C) -5 D)
B) 3 C) -5 D) 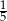
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 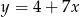 jest równy
jest równy
A) 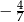 B)
B) 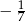 C) 7 D)
C) 7 D) 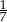
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 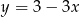 jest równy
jest równy
A) 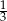 B) 3 C) -3 D)
B) 3 C) -3 D) 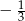
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 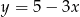 jest równy
jest równy
A) 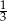 B) -3 C) 5 D)
B) -3 C) 5 D) 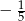
Prosta 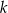 ma równanie
ma równanie 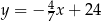 . Współczynnik kierunkowy prostej prostopadłej do prostej
. Współczynnik kierunkowy prostej prostopadłej do prostej 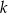 jest równy
jest równy
A)  B)
B) 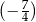 C)
C) 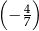 D)
D) 
Prosta 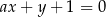 jest równoległa do prostej
jest równoległa do prostej 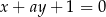 . Wtedy
. Wtedy
A) 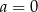 B)
B) 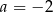 C)
C) 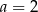 D)
D) 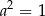
Prosta 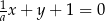 jest równoległa do prostej
jest równoległa do prostej 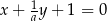 . Wtedy
. Wtedy
A) 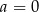 B)
B) 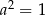 C)
C) 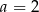 D)
D) 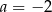
Punkty 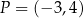 i
i 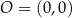 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem jaki tworzy ta prosta z ujemną półosią
jest kątem jaki tworzy ta prosta z ujemną półosią 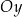 (zobacz rysunek).
(zobacz rysunek).
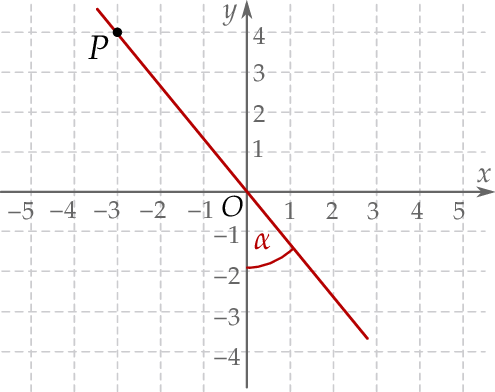
Wtedy tangens kąta  jest równy
jest równy
A) 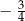 B)
B) 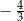 C)
C)  D)
D)