Zadanie nr 1613401
Wiadomo, że liczba 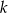 jest liczbą naturalną dodatnią i liczby
jest liczbą naturalną dodatnią i liczby 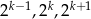 są trzema początkowymi wyrazami ciągu geometrycznego
są trzema początkowymi wyrazami ciągu geometrycznego 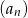 , gdzie
, gdzie 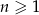 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 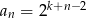 B)
B) 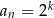 C)
C) 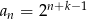 D)
D) 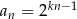
Rozwiązanie
Z założeń mamy
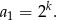
Aby wyznaczyć wyraz ogólny wystarczy policzyć iloraz
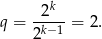
Teraz już łatwo zapisać wzór na wyraz ogólny
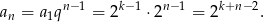
Odpowiedź: A

