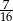O zdarzeniach losowych 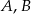 wiadomo, że:
wiadomo, że: 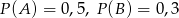 i
i 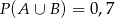 . Prawdopodobieństwo iloczynu zdarzeń
. Prawdopodobieństwo iloczynu zdarzeń 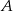 i
i 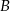 spełnia warunek
spełnia warunek
A) 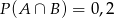 B)
B) 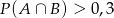 C)
C) 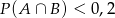 D)
D) 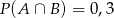
/Szkoła średnia/Zadania testowe/Prawdopodobieństwo
Wiadomo, że 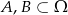 oraz
oraz 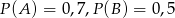 i
i 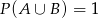 . Zatem
. Zatem
A) 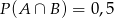 B)
B) 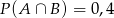 C)
C) 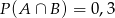 D)
D) 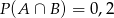
O zdarzeniach losowych 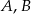 wiadomo, że:
wiadomo, że: 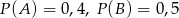 i
i 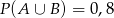 . Prawdopodobieństwo iloczynu zdarzeń
. Prawdopodobieństwo iloczynu zdarzeń 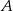 i
i 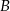 spełnia warunek
spełnia warunek
A) 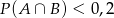 B)
B) 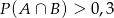 C)
C) 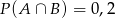 D)
D) 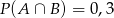
Wiadomo, że 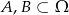 ,
, 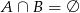 ,
, 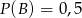 oraz
oraz 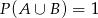 . Zatem
. Zatem
A) 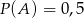 B)
B) 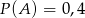 C)
C) 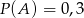 D)
D) 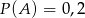
Wiadomo, że 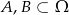 oraz
oraz 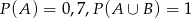 i
i 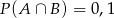 . Zatem
. Zatem
A) 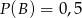 B)
B) 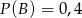 C)
C) 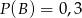 D)
D) 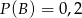
O zdarzeniach losowych 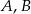 wiadomo, że:
wiadomo, że: 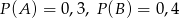 i
i 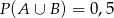 . Prawdopodobieństwo iloczynu zdarzeń
. Prawdopodobieństwo iloczynu zdarzeń 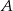 i
i 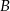 spełnia warunek
spełnia warunek
A)  B)
B) 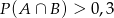 C)
C) 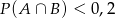 D)
D) 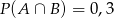
Ze zbioru liczb całkowitych, które są zawarte w przedziale 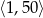 losujemy dwa razy po jednej liczbie (wylosowany liczby mogą się powtarzać). Prawdopodobieństwo zdarzenia polegającego na tym, że jedna z wylosowanych liczb jest kwadratem drugiej liczby jest równe:
losujemy dwa razy po jednej liczbie (wylosowany liczby mogą się powtarzać). Prawdopodobieństwo zdarzenia polegającego na tym, że jedna z wylosowanych liczb jest kwadratem drugiej liczby jest równe:
A) 0,0048 B) 0,0028 C) 0,0024 D) 0,0052
Rzucamy jeden raz symetryczną sześcienną kostką do gry. Niech 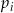 oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez
oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez 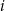 . Wtedy
. Wtedy
A) 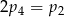 B)
B) 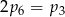 C)
C) 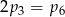 D)
D) 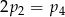
Rzucamy jeden raz symetryczną sześcienną kostką do gry. Niech 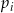 oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez
oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez 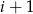 . Wtedy
. Wtedy
A) 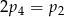 B)
B) 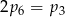 C)
C) 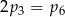 D)
D) 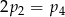
Z wierzchołków sześcianu 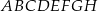 losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześcianu
losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześcianu 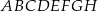 , jest równe
, jest równe
A) 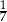 B)
B) 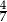 C)
C) 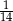 D)
D) 
Z wierzchołków sześcianu 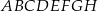 losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te są końcami przekątnej jednej ze ścian sześcianu
losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te są końcami przekątnej jednej ze ścian sześcianu 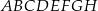 , jest równe
, jest równe
A) 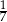 B)
B) 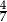 C)
C) 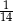 D)
D) 
Zdarzenie 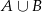 jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia
jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia 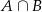 jest równe
jest równe 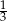 . Wobec tego suma prawdopodobieństw zdarzeń
. Wobec tego suma prawdopodobieństw zdarzeń 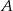 i
i 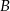 jest równa
jest równa
A) 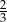 B)
B) 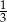 C) 1 D)
C) 1 D) 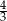
Zdarzenie 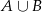 jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia
jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia 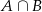 jest równe
jest równe 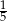 . Wobec tego suma prawdopodobieństw zdarzeń
. Wobec tego suma prawdopodobieństw zdarzeń 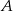 i
i 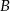 jest równa
jest równa
A) 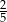 B)
B) 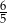 C) 1 D)
C) 1 D) 
Rzucamy dwa razy sześcienną kostką do gry. Niech 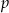 oznacza prawdopodobieństwo tego, że iloczyn liczb otrzymanych oczek dzieli się przez 6. Wtedy
oznacza prawdopodobieństwo tego, że iloczyn liczb otrzymanych oczek dzieli się przez 6. Wtedy
A) 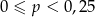 B)
B) 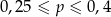 C)
C) 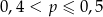 D)
D) 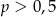
Ze zbioru pięćdziesięciu kolejnych liczb naturalnych od 1 do 50 losujemy dwie liczby  i
i 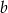 takie, że
takie, że 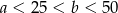 . Prawdopodobieństwo, że liczba
. Prawdopodobieństwo, że liczba 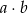 jest podzielna przez 50 jest równe
jest podzielna przez 50 jest równe
A) 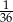 B)
B) 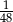 C)
C) 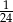 D)
D) 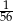
Mamy cztery urny. W urnie o numerze 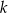 , dla
, dla 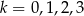 znajduje się
znajduje się 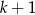 kul białych i
kul białych i 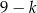 kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z
kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z 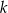 oczkami,
oczkami, 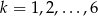 to losujemy jedną kulę z urny, której numer jest równy reszcie z dzielenia liczby
to losujemy jedną kulę z urny, której numer jest równy reszcie z dzielenia liczby 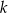 przez 4. Prawdopodobieństwo wylosowania kuli białej jest równe
przez 4. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 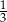 B)
B) 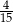 C)
C) 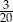 D)
D) 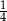
Ze zbioru kolejnych liczb naturalnych 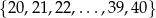 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe
A) 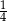 B)
B) 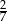 C)
C) 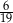 D)
D) 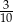
Ze zbioru kolejnych liczb naturalnych 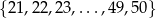 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 6 jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 6 jest równe
A) 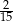 B)
B)  C)
C) 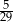 D)
D) 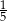
W pudełku znajdują się tylko kule białe i czarne. Stosunek liczby kul białych do liczby kul czarnych jest równy 3:4. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania białej kuli jest równe
A)  B)
B)  C)
C) 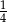 D)
D) 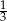
W pudełku znajdują się tylko kule białe i czarne. Stosunek liczby kul czarnych do liczby kul białych jest równy 4:5. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania białej kuli jest równe
A)  B)
B)  C)
C) 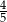 D)
D) 
W pudełku znajdują się tylko kule białe i kule czerwone. Stosunek liczby kul białych do liczby kul czerwonych jest równy 3:4. Wylosowanie każdej kuli z tego pudełka jest jednakowo prawdopodobne. Losujemy jedną kulę. Niech 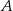 oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia 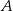 jest równe
jest równe
A) 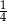 B)
B) 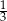 C)
C) 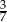 D)
D) 
W pudełku znajdują się tylko kule białe i kule czerwone. Stosunek liczby kul białych do liczby kul czerwonych jest równy 4:5. Wylosowanie każdej kuli z tego pudełka jest jednakowo prawdopodobne. Losujemy jedną kulę. Niech 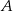 oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia 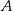 jest równe
jest równe
A) 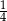 B)
B) 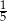 C)
C) 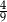 D)
D) 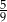
W pojemniku są wyłącznie kule białe i czerwone. Stosunek liczby kul białych do liczby kul czerwonych jest równy 4 : 5. Z pojemnika losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 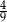 B)
B)  C)
C) 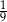 D)
D) 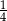
W woreczku są tylko koraliki białe i czerwone. Białych koralików jest cztery razy więcej niż czerwonych. Losujemy jeden koralik. Prawdopodobieństwo, że wylosujemy biały koralik, jest równe
A) 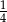 B)
B) 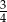 C)
C) 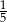 D)
D) 
Zdarzenia losowe 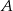 i
i 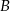 są rozłączne oraz
są rozłączne oraz 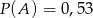 . Zatem prawdopodobieństwo zdarzenia
. Zatem prawdopodobieństwo zdarzenia 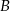 może być równe
może być równe
A) 0,63 B) 0,53 C) 0,43 D) 1
Zdarzenia losowe 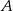 i
i 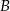 są rozłączne oraz
są rozłączne oraz 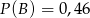 . Zatem prawdopodobieństwo zdarzenia
. Zatem prawdopodobieństwo zdarzenia 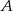 może być równe
może być równe
A) 0,63 B) 0,53 C) 0,73 D) 1
Prawdopodobieństwo zalezienia wśród 99 uczniów piętnastu, który urodzili się tego samego dnia tygodnia jest równe
A) 0 B) 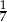 C)
C) 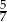 D) 1
D) 1
Człowiek na głowie posiada mniej niż 200 tys. włosów. Prawdopodobieństwo, że w mieście liczącym ponad 200 tys. mieszkańców znajdą dwie osoby, które mają dokładnie tyle samo włosów na głowie wynosi
A) 1 B) 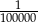 C)
C) 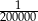 D) 0
D) 0
Rzucamy dziewięć razy symetryczną monetą. Niech 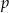 oznacza prawdopodobieństwo otrzymania co najwyżej 8 orłów w tych dziewięciu rzutach. Wtedy
oznacza prawdopodobieństwo otrzymania co najwyżej 8 orłów w tych dziewięciu rzutach. Wtedy
A) 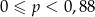 B)
B) 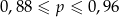 C)
C) 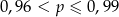 D)
D) 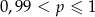
Ze zbioru liczb 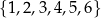 losujemy dwa razy po jednej liczbie ze zwracaniem. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
losujemy dwa razy po jednej liczbie ze zwracaniem. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wylosowania dwóch liczb, których suma dzieli się przez 9 jest większe od 0,1. | P | F |
| Prawdopodobieństwo tego, że pierwsza liczba dzieli drugą jest mniejsze niż 0,38. | P | F |
Rzucamy czterokrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że suma oczek wyrzuconych w czterech rzutach jest różna od 23 jest równe
A) 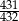 B)
B) 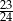 C)
C) 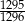 D)
D) 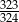
O zdarzeniach losowych 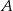 i
i 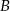 zawartych w
zawartych w 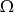 wiadomo, że
wiadomo, że 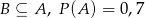 i
i 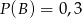 . Wtedy
. Wtedy
A) 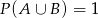 B)
B) 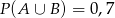 C)
C) 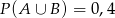 D)
D) 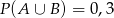
O zdarzeniach losowych 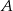 i
i 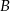 zawartych w
zawartych w 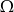 wiadomo, że
wiadomo, że 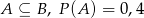 i
i 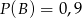 . Wtedy
. Wtedy
A) 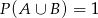 B)
B) 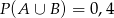 C)
C) 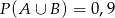 D)
D) 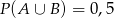
O zdarzeniach losowych 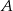 i
i 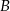 zawartych w
zawartych w 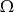 wiadomo, że
wiadomo, że 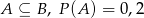 i
i 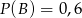 . Wtedy
. Wtedy
A) 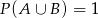 B)
B) 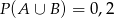 C)
C) 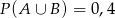 D)
D) 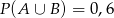
Niech 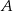 i
i 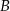 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 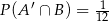 i
i 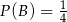 . Wtedy prawdopodobieństwo warunkowe
. Wtedy prawdopodobieństwo warunkowe 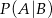 jest równe
jest równe
A) 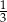 B)
B) 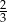 C)
C) 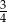 D)
D) 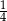
Niech 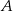 i
i 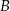 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 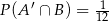 i
i 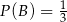 . Wtedy prawdopodobieństwo warunkowe
. Wtedy prawdopodobieństwo warunkowe 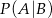 jest równe
jest równe
A) 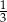 B)
B) 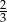 C)
C) 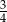 D)
D) 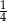
W klasie liczącej  osób, w tym 12 dziewcząt, wybrano losowo jedną osobę. Prawdopodobieństwo, że jest to chłopiec jest równe
osób, w tym 12 dziewcząt, wybrano losowo jedną osobę. Prawdopodobieństwo, że jest to chłopiec jest równe  , zatem:
, zatem:
A) 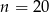 B)
B) 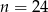 C)
C) 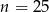 D)
D) 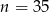
W klasie liczącej  osób, w tym 7 dziewcząt, wybrano losowo jedną osobę. Prawdopodobieństwo, że jest to chłopiec jest równe
osób, w tym 7 dziewcząt, wybrano losowo jedną osobę. Prawdopodobieństwo, że jest to chłopiec jest równe  , zatem:
, zatem:
A) 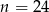 B)
B) 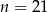 C)
C) 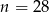 D)
D) 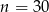
W pudełku są 4 kule białe i  kul czerwonych. Prawdopodobieństwo wylosowania kuli czerwonej jest równe
kul czerwonych. Prawdopodobieństwo wylosowania kuli czerwonej jest równe  , gdy
, gdy
A) 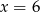 B)
B) 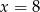 C)
C) 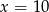 D)
D) 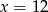
Z pudełka, w którym jest tylko 8 kul białych i  kul czarnych, losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli czarnej jest równe
kul czarnych, losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli czarnej jest równe  . Liczba kul czarnych jest równa
. Liczba kul czarnych jest równa
A) 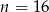 B)
B) 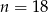 C)
C) 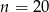 D)
D) 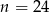
Z pudełka, w którym jest tylko 6 kul białych i  kul czarnych, losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli białej jest równe
kul czarnych, losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli białej jest równe 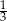 . Liczba kul czarnych jest równa
. Liczba kul czarnych jest równa
A) 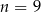 B)
B) 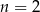 C)
C) 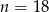 D)
D) 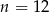
W pudełku jest 5 kul czerwonych i  kul żółtych. Prawdopodobieństwo wylosowania kuli żółtej jest równe
kul żółtych. Prawdopodobieństwo wylosowania kuli żółtej jest równe  , gdy
, gdy
A) 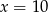 B)
B) 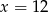 C)
C) 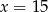 D)
D) 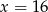
Rzucamy trzy razy symetryczną monetą. Prawdopodobieństwo otrzymania co najmniej jednej reszki jest równe
A)  B)
B) 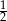 C)
C) 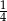 D)
D) 
Rzucamy cztery razy symetryczną monetą. Prawdopodobieństwo otrzymania co najmniej jednego orła jest równe
A)  B)
B) 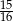 C)
C) 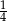 D)
D)